Pitcher Height Comparison- Velocity, Elbow Injuries, & Mechanics

It’s a debate that’s as old as time – are taller pitchers truly better than shorter pitchers? Do they stay healthier? Can they throw harder with less effort?
Analysts like David Cameron have said:
There is validity to the belief that shorter pitchers have a smaller margin for error. In order to generate the same power as a pitcher with more natural strength, they can tend to put more pressure on their arms, thus leading to poor mechanics and eventual injuries.
Glenn P. Greenberg thoroughly researched this topic for SABR in the Fall 2010 Baseball Research Journal, and came away with a ton of interesting findings, most notably:
- …the data indicate that height is essentially irrelevant when a pitcher is good enough to become an established major-league pitcher.
- While drafted shorter players are just as likely to become established major-league relief pitchers and established major-league pitchers in general, taller pitchers are more likely to become established major-league starting pitchers.
- …the conclusion that makes the most sense is that the reason for the statistically significant correlation between height and becoming an established major-league starting pitcher is opportunity rather than any difference due to genetics.
- These data demonstrate that there is no statistical evidence that shorter pitchers are more or less durable than taller pitchers.
Basically, shorter pitchers are as good as taller pitchers, but they are afforded fewer opportunities to become major league starting pitchers simply due to bias by coaches and front office members. My anecdotal experience from working in professional baseball as a scouting analyst and player development consultant lends support to this theory; coaches in general do not believe shorter pitchers can be successful big league starting pitchers, with anyone short (Stroman, Lincecum) doing well being labeled as pure exceptions, freaks, and so forth.
The sabermetric analytical look into the data is very interesting, but there are still a number of myths and concepts that continue to be brought up that have not as of yet been thoroughly discussed. Let’s take a look at angular velocity of the pitching arm and the varying stress a taller, longer-limbed pitcher might suffer compared to a shorter one.
Angular Velocity and Distal-Proximal Displacement Variation
Here’s a basic but rather deep question:
Does the outside of a wheel spin at the same speed as the inside of the wheel?
If you watch a point on the blue line closer to the center of the wheel compared to a point on the blue line on the outside of the wheel, it becomes readily apparent that the point on the outside of the wheel is actually moving faster! This is a somewhat unintuitive concept in physics related to angular velocity. The velocity of any given point on a wheel can be calculated using the formula:
v = 2πr * f
- v = velocity
- π = pi, or 3.14159…
- r = radius (or in this case, the distance from the center of the wheel, 0 being the center, and the full radius R being the rim of the wheel)
- f = frequency, or number of revolutions the wheel makes
The frequency of the wheel is the same throughout – the entire wheel rotates together. But varying points ON the wheel’s radius clearly do not have the same speed.
So how is this related to pitching?
Arm Speed and Kinematics
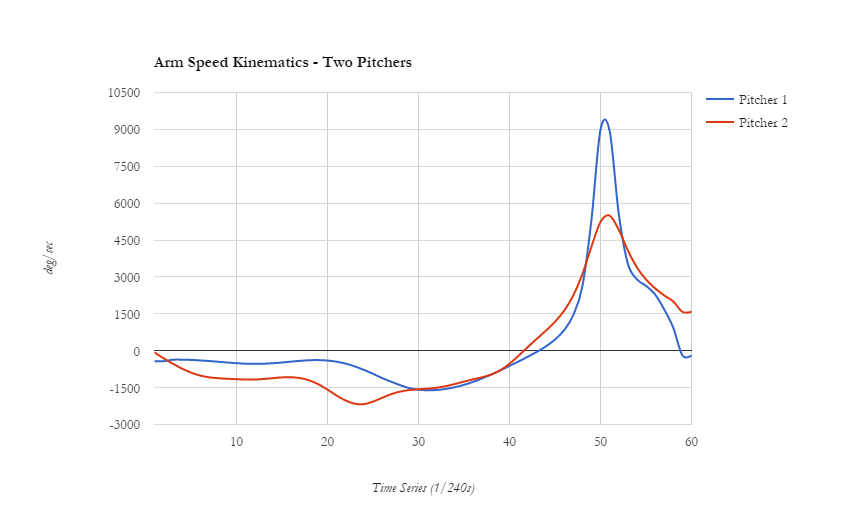
Take for example this chart of two professional pitchers analyzed in the Driveline Biomechanics Laboratory using multiple high-speed cameras and a direct linear transformation method… (I’ll skip the rest, but if you want to read the OG paper on the topic, Dynamics of the Shoulder and Elbow Joints of the Throwing Arm During a Baseball Pitch by Feltner and Dapena is what you’re looking for)
In this case, “arm speed” is actually the internal rotation of the shoulder. This is what it looks like:
There are a few things to note in the graph above. Here are a few that are relevant to the discussion at hand:
- Pitcher 1 has a much higher internal rotation angular velocity peak
- Pitcher 1 has a much steeper slope in both acceleration and deceleration in internal rotation
- Pitcher 2 begins internal rotation acceleration sooner than Pitcher 1
Hold your arm up so that your elbow is at the height of your shoulder and your hand is pointing upwards. Internally rotate your shoulder by driving the hand palm down towards the ground. Do it again. If you could somehow rotate it 360 degrees, that’d be a wheel, right? See where this is going?
Now, a pitcher with longer elbow to fingertip length (“forearm length”) in theory can angularly internally rotate their arm much slower than one with shorter forearm length to create equal ball speed, because remember, the longer the lever, the greater the potential there is to create speed at the end of the radius. This is immediately understandable if you have a sledgehammer with a very long handle – you don’t have to swing it hard to create serious speed at the end. Compare that to a sledgehammer with a shorter handle where you have to put in more effort to create distal hammer speed.
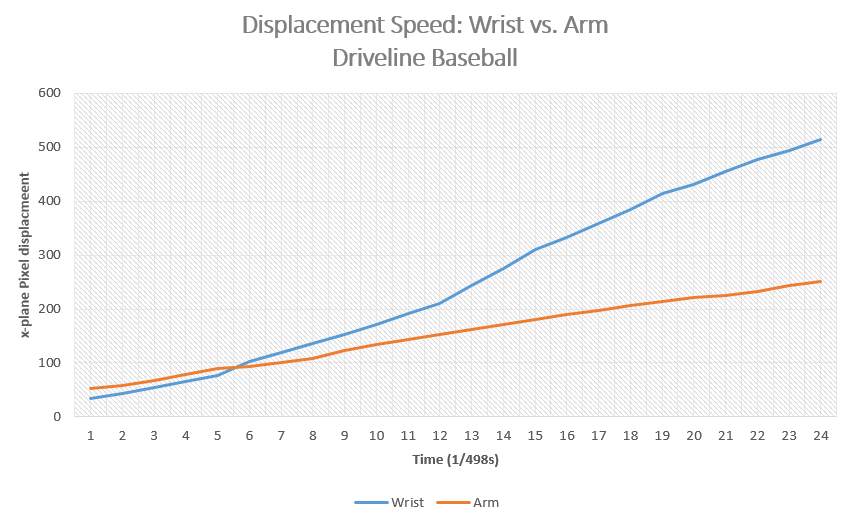
Take a look at Matt Boyd throwing a flat ground fastball – markers have been imperfectly placed at the wrist and closer to the proximal humerus. You can see the wrist’s velocity overtake the arm’s velocity rather fast – graphed for your convenience below the GIF:
So, taller pitchers and longer-limbed pitchers are at a clear advantage, right?
Come on. You didn’t think it was going to be this easy, did you?
The Long-Limbed Tradeoff: Torque and Control
Let’s go back to sledgehammer example – the longer the handle, the less speed you need to create at the center to result in distal implement speed (end of the hammer). In the pitching delivery, this sounds good – to generate elite ball velocity, a longer-limbed (usually taller) pitcher needs less gross internal rotation angular velocity than a shorter-limbed (usually shorter) pitcher. But this does not describe stress to the joints and soft tissues (UCL) that support the elbow. Torque is generally accepted as a measure of stress in human kinematics.
The formula for torque is:
Torque = F × Df
- Torque = Stress
- F = force (mass * acceleration)
- Df = distance to the fulcrum (in this case, the elbow in our simplified model)
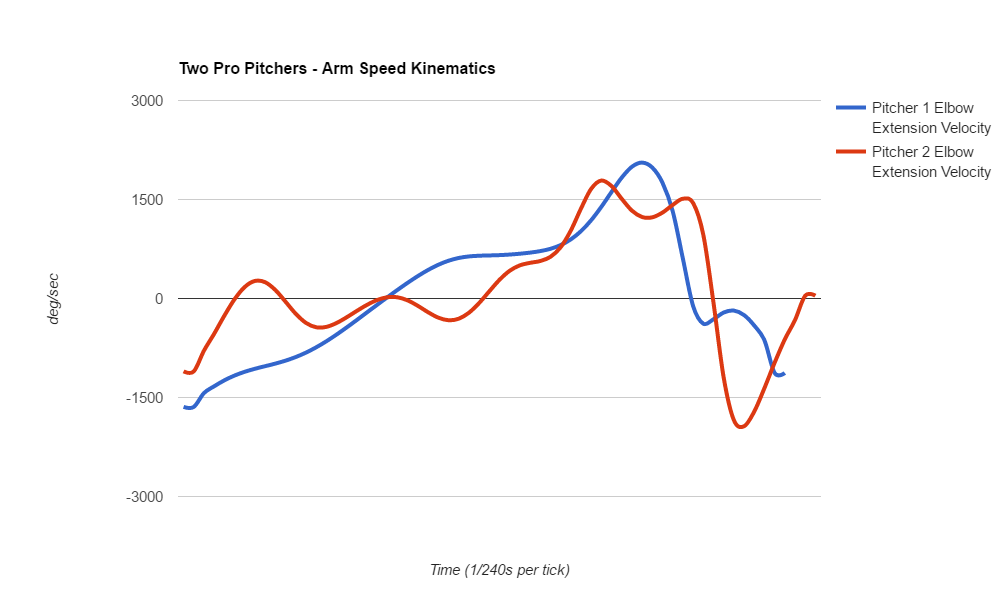
Remember the graph above on internal rotation and the notes about how Pitcher 1 has much higher internal rotation angular acceleration than Pitcher 2? Here’s something else about Pitcher 1 – he is a full 6 inches taller than Pitcher 2 and has significantly longer limbs! Therefore, it’s safe to say that Pitcher 1 is creating far more torque and stress on the arm from a purely mechanical look at the arm. The mass of the baseball is 5 oz and Pitcher 1’s acceleration was higher, therefore F was much higher AND Df was much higher since he has a longer forearm.
But that’s not all. Imagine that you have a dowel rod that is 7 feet long and you raise it upwards over your head and swing it downwards in an ax-chopping motion at a target on the ground as fast as you can. Now mentally see yourself swinging a 3-foot dowel rod. You swing both 20 times each and record the location at which you hit the ground in front of you. Which grouping will be tighter around the target? The 3-foot dowel rod is significantly easier to control because the margin for error grows larger and larger with the length of the rod. The forearm in the pitching delivery is not staying on the same plane while the arm is internally rotating, the elbow is flexing/extending at the same time, and the longer the forearm, the more the tips of the fingers are displaced due to a single degree of change to flexion/extension at the elbow – and the elbow bends and straightens fast in the delivery.
From a purely mechanical look at pitching, the taller pitcher not only has the potential to have worse command problems due to the length of the forearm (not to mention the humerus), but also has a higher multiplier for torque and therefore stress on the structures of the human body.
CONCLUSION: Efficiency of Angular Velocity
I’ll end this post with something that will really blow your mind. Let’s take a look at the internal rotation angular velocity graph that kicked this post off:
Again, here’s what we know about the two pitchers:
- Pitcher 1 is taller and has longer limbs than Pitcher 2
- Pitcher 1 creates more “arm speed” in both internal rotation AND elbow extension than Pitcher 2
- Pitcher 1 weighs more and is stronger by all strength-based metrics
Taller, faster arm, weighs more and is stronger. Therefore, we can clearly conclude that Pitcher 1 threw a faster pitch than Pitcher 2 in this trial, right?
Wrong. Pitcher 1 and Pitcher 2 both threw a fastball at 88 MPH in this trial, and the difference between their measurements is very significantly different even factoring in measurement error from our lab metrics.
How could that be possible? It literally seems impossible, right?
The efficiency of arm speed is likely a real factor – remember that so-called “velocity” as used by baseball is really “speed,” because velocity has not only a speed component but a vector (directionality) component. Does the pitcher actually “use” his arm speed efficiently to create final ball velocity? Are some better at it than others, and if so, what kinematic measures are those?
And that, my friends, is something no one truly knows. So when your coaches have definitive answers as to how fastball velocity is really created, just remember, they probably don’t.
Or they know something that literally no one else does. In which case, have them email me.
Want to learn more about what we know about gaining fastball velocity? Check out the wide array of blog articles we have relating to velocity building here.
Comment section
Add a Comment
You must be logged in to post a comment.


John mcmillan -
I’d imagine core speed has as much to do with ball velocity, if not more than arm/shoulder strength. Compare the body to a trebuchet. The arm & sling are both static (no muscles in them) – it’s the weight pulling the whole mechanism down that transmits the force. The trebuchet arm just needs to be simply stiff and not break and yet have flex to store and release energy.
So a strong core that can snap quickly is the key – plyometric training is a must. I guess that’d be fast-twitch muscle fibers one wants to encourage growth of.
It’s why some flame throwers like Verlander have core muscle tears that need surgery.
Some that lose velocity might not know why but the issue might lie in core muscle weakness from damage or age.
Kyle Boddy -
The problem is that if core speed is important, it alone does not propel the ball. Core speed would contribute to arm angular velocity and it would show up in “arm speed” regardless.
John mcmillan -
Of course falling off the mound helps too but it’s the whole system in play. A strong core shouldn’t be minimized. Try ringing the bell at the circus with just your arms then do it using your core. You’ll see a vast difference.
Kyle Boddy -
Well, yeah. No one is disputing that. I’m just saying core rotational angular velocity will show up in arm speed.
John mcmillan -
The whole point is finding the secret to increased velocity that you reference. More intense but well managed workouts for the core will do more to result in increased velocity than any other one thing.
Look at it as a space ship using the gravity of the Sun to whip around to get somewhere farther and faster. The ship (ball) has it’s own rocket engine (arm) but with the addition of the Sun’s gravity (the core) the gain is exponential.
Kyle Boddy -
You are basically talking to yourself at this point.
Tommy -
Josh,
What exact core exercises would help with velocity? Or atleast what specific ones…
Steve Park -
Hi Kyle,
How do you measure core speed and it’s contribution to arm velo?
Thanks,
Steve
Tyler W -
Take both pitchers and follow a similar data gathering protocol, except have them try their best to disassociate their core/lower half from the upper half. I’d be interested to see their arm speed/ball velocity comparing both. Maybe put them in a rolling chair with their feet up, take as much ground force out of it.
dan -
slightly unrelated but how do the spin rates compare for these two pitchers
Greg -
What is the height range for short pitchers? Tall pitchers?
Tavis Bruce -
Hi Kyle,
Just got around to reading this. Nice post!
Quick question for you: Is the kinematic data you’ve presented here synchronized to the instant of ball release?
Cheers,
Tavis
Scott -
Kyle,
The efficiency of applying the force through the fingers into the ball seems to be very relevant. One of the pitchers may be off center of the ball.
Tommy -
Scott,
Do you have any drills to increase using your fingers more? Or is it just thinking about using your fingers at release more…
What Long-Term Velocity Development Looks Like: The Herbie Good Story - Driveline Baseball -
[…] training stand-point, Herbie had huge hurdles to overcome on the strength and coordination fronts. Tall athletes generally present coordination challenges. Doing Herbie’s initial assessment, the two most glaring issues were major general strength […]
Matt Hopkinson -
Is it simply physics cancelling each other out. One has smaller levers and better control and therefore purer force transference. The other longer levers and strength but less control and therefore energy wastage and probably increased likelihood for injury.
Interesting in this day and age there is still a bias based on size and handedness and somatotype rather than just outcomes. You throw hard and accurately or you don’t.
How to Use the Motus Sleeve - Driveline Baseball -
[…] because studies have shown that both height and weight have a relationship to arm torque. We have mentioned this before in previous articles, but taller athletes are most likely going to have longer arms when compared to shorter athletes, […]
Nick -
Not sure if you still see these but I have been reading more on pitching studies and am wondering if the data can be trusted with lower velocity throwers like this? With so many factors involved, it seems like a minimum threshold for velocity in studies would maybe take away some of the variables as throwing 90+ requires a certain level of mechanical proficiency. Freaks obviously are not great for studies either.
Thanks so much for putting out all this great content.