Optimizing Breaking Ball Shape Through Data-Driven Pitch Design, Part One
Written by Sam Bornstein
With technologies like Rapsodo, TrackMan, and Yakkertech reaching the mainstream in recent years, designing a specific breaking ball for an athlete has never been more straightforward to accomplish.
Big leaguers are using advances in Pitch Design to their advantage to increase velocity and add additional sweep and depth to their breaking balls, helping them achieve a record number of strikeouts in the process.
Of course, we know that we’ve always been striving for more sweep, more depth, and more velocity with breaking balls, and, as a function of that, the league’s average slider has only gotten nastier over time. But, let’s consider a more likely scenario: what if adding sweep to a breaking ball comes with a loss of velocity, or adding velocity comes with a loss of depth and spin efficiency?
How do we optimize the three components of improving a breaking ball while being cognizant of the nuanced tradeoff between them all?
In this blog, we’ll try to tackle some of those hard hitting questions by providing context using MLB data and Driveline’s internal models—models we use with our own high-level athletes in Pitch Design sessions. This will be part one of a two-part breaking ball pitch design blog series.
The hope here is that the reader can put these insights into play within their own Pitch Design sessions to design more effective breaking balls with their athletes.
The Breaking Ball Spectrum
An athlete can fashion a breaking pitch in many shapes to achieve the desired movement and spin pattern. Sticking to traditional classifications, the spectrum of glove-side pitches includes cutters, sliders, and curveballs.
A cutter, also known as a “cut-fastball”, is thrown with higher velocity, less horizontal break and more vertical carry than a slider or curveball. It gets its name from the sharp, “cutting” action it moves with. The pitch mostly moves with backspin and gyrospin, which is how the velocity is generated. Sometimes, sidespin is mixed in, and depending on how much, the pitch becomes a hybrid between a slider and a fastball. For some pitchers, a cutter is their primary offering because of how hard they can throw it.
A slider is a cutter’s close neighbor. Traditionally thrown with more sidespin than backspin, the pitch traditionally breaks glove-side with more lateral sweep than cutters (gyro-dominant sliders excluded). Because it balances the three spin components, sliders come in many different shapes and sizes, and the amount of sweep is often the focal point of the shape.
Curveballs are thrown with the most downward movement of the three breaking balls. This depth is achieved by adding topspin to the release of the pitch. There is less diversity in curveball shapes; the most common types have straight downward movement—a 12-6 curveball—or “slurvy” action, where it is thrown with equal parts negative horizontal break and vertical break.
Above are the 2021 MLB averages for velocity, vertical break, (normalized) horizontal break, and spin efficiency for fastballs, cutters, sliders, and curveballs. As we move across the breaking ball velocity spectrum, there’s an increase in horizontal sweep, which we can refer to as the velocity-sweep tradeoff, along with an increase in depth.
Putting Breaking Balls Into Context
Given that a trade-off between velocity and movement exists on breaking balls, one of the first things we like to do at Driveline is put a player’s breaking ball into context relative to league-wide expectation.
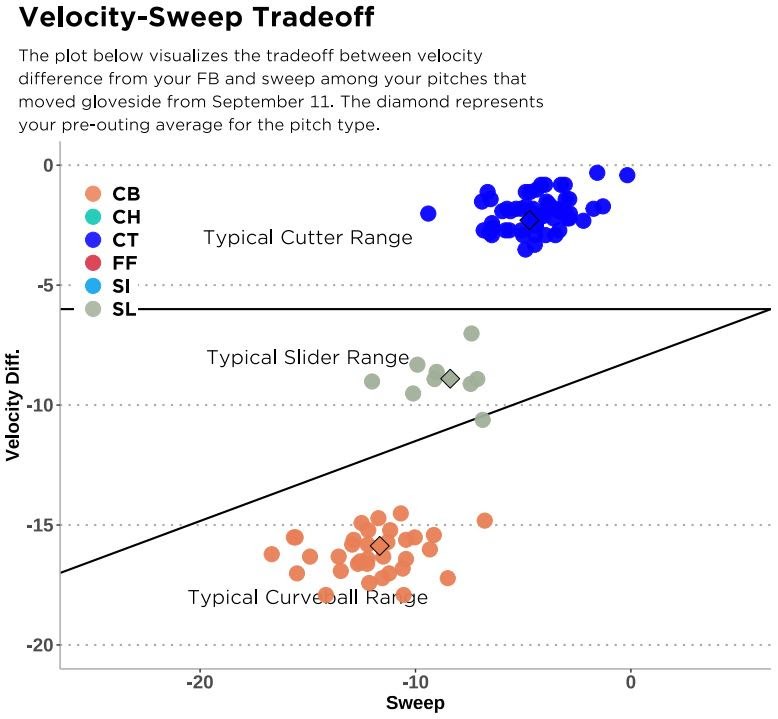
For example, depicted in the visualization above is Corbin Burnes’ no-hit outing from September 11th, where we can see that all three of his breaking pitches — the CT, SL, and CB — all fell within the relative sweep-velocity tradeoff regions we’d expect a big leaguer to land in.
While relatively unsurprising given how successful all three pitches play on a per-outing basis, the visualization above becomes more important—even critical—when evaluating the breaking balls of amateur and lower level players, given that it helps us scale a player’s feel for throwing a breaking ball relative to their FB velocity.
So, rather than using a pitch model to harshly grade a 77 mph gyro-SL because it’s 77 mph, the visualization above can help scale this hypothetical pitch for an athlete that throws 84 mph and put the pitch in better context.
By showing an athlete that their SL actually falls in-line with big league expectations, and just doesn’t have sharpness because they throw 84 mph with their FB, you can give the athlete some peace of mind. They know that their SL is fine as is, and that FB velocity is the main thing keeping them from throwing a quality breaker.
A trainer or coach can program a bit more optimally knowing that multiple pitch design sessions with the breaking ball aren’t a must if the FB velo ticks up.
Expecting a Given Velocity Drop
To more precisely evaluate a player’s breaking ball, we built a model to estimate each pitch’s expected velocity differential from the pitcher’s fastball, based on the spin-components of the breaking ball, characteristics of the fastball, and arm angle of the pitcher.
To visualize how each of Burnes’ breaking balls differ in velocity from his fastball, we plotted them with their spin direction on a polar coordinate graph. The actual velocity differentials are plotted on the left below and the expected differentials from our model are plotted on the right.
In 2021, Burnes has averaged a drop of 1.6 mph on his cutter, but our model expects him to drop 4.0 mph. Thus, Burnes gains 2.4 mph more than expected on the pitch. On the other hand, his curveball loses 3.9 mph more than the expected 11.7 mph differential, dropping 15.6 mph on average. Lastly, his slider velocity differential is nearly identical to his expected loss at 8.9 mph.
To no surprise, the cutter is Burnes’ most used pitch, and, in terms of intrinsic run values since 2020, his best pitch, followed by the slider and curveball. Per our Stuff+ model, these pitches have scores of 172, 155, and 91, respectively.
If the stellar right-hander has an area to improve, there is potentially some room to add a few miles per hour back onto the curveball to become even more effective, assuming that the pitch doesn’t then blend in with his SL. But, as we stated previously, velocity often cannot be increased without some tradeoff.
The Practical Component of a Velo-Movement Tradeoff
To illustrate how players can work around their own Velo-Movement trade-off, let’s consider a pitcher who increased his slider velocity between seasons.
Houston Astros right-handed pitcher Cristian Javier enjoyed a nice rookie season in 2020 and has continued that success into this year. Javier increased his slider velocity 2.8 mph from 2020 to 2021, one of the largest increases across the league.
Javier’s slider in 2020 was a more traditional lateral sweeper with 13.2 inches of glove-side movement and 2.3 inches of vertical break at 78.6 mph. The 2021 version of this pitch shortened up a bit, losing 3 inches of sweep and gaining 2.3 inches of carry in the process, as well as the 2.8 mph velocity gain.
While the velocity gain and subsequent loss in movement from season to season illustrates the tough give and take in breaking ball pitch design, this tradeoff observed is exactly what we’d expect given the change in spin profile, according to our expected velo-drop model.
In other words, given that we know how much velocity Javier would gain or lose by shortening or lengthening the shape of his breaking ball via a model, we can create more realistic pitch design goals with athletes and chase an optimal shape that is individualized for each player.
It seems as though the Astros have similar insights, given that both versions of Javier’s sliders have performed pretty well against big league hitters. Not all tradeoffs have negative consequences; it’s about optimizing where the breaking ball is most effective and understanding how each athlete adapts to these adjustments.
Finding Areas of Improvement
While we’ve demonstrated use-cases for when an expected movement/velo tradeoff model can be used for athletes with high feel for spin, the model can also identify pitchers with breaking ball velocity differentials that are below league expectation.
Trevor Rogers
The Miami Marlins’ All-Star pitcher possesses a slider that loses more velocity from his fastball than we expect. Here is his arsenal at this point in the season.
While the left-hander possesses a pretty lights-out CH, his breaking ball has a high degree of gyro spin, which doesn’t give it much carry or sweep. Thrown at 81.8 mph, it drops 12.6 mph from his 94.9 mph heater, 4.9 mph more than the 7.7 mph drop we’d expect given the spin profile. This same pitch at 87 mph could be dramatically more effective, and we would only guess that it would be used more often than 15% of the time.
Previously, we plotted Burnes’ breaking ball velocity differentials on a polar coordinate graph with each pitch’s spin direction. We saw that each pitch’s actual velocity drop lined up fairly well with its expected difference. With Rogers, the opposite is true.
Due to its gyro spin, his slider lives all around the 360-degree axis. Those pitches that back up on him have smaller expected differentials because they do not break gloveside much, and spin in the same direction as his fastball.
Despite the phenomenal season he’s putting together in 2021, he relies on his four-seam fastball and changeup 85% of the time. Mixing in a harder gyro-slider or a brand new sweeping slider with the expected velocity differential could make Rogers all the more successful against big league hitters.
Chris Bassitt
Bassitt throws two times the number of pitches that Rogers does, carrying an arsenal of six pitches that have a wide spectrum of velocities. The Oakland A’s right-hander pairs his hard, sharp cutter with two significantly slower breaking balls.
The all-star pitcher’s slider and curveball are 15.9 mph and 21.2 mph slower, respectively, than his average fastball velocity. For pitchers with both FF and SI, our model uses the average velocity of these two combined to find the differential values. Bassitt’s SL and CB are approximately league average in terms of our Stuff+ model this season, and we noticed an interesting adjustment he made with his slider within the last couple months.
Since mid-June, the slow sweeper is steadily becoming a harder, shortened version of the pitch. Pitches with less sweep are typically thrown a bit faster, as per the velocity-sweep tradeoff, so Bassitt is likely in the midst of making said tradeoff, whether intentional or not.
As the slider becomes closer in velocity to the cutter, the curveball lags behind in speed and becomes a freeze pitch by nature. The usage rate and location of the pitch becomes even more important to maintain its success at such a low velocity.
With three breaking balls and six total pitches in the fold, it’s difficult to formulate the proper usage of each pitch. The slider and curveball are two of his lesser-used pitches, so the less than average velocity expectation could be a product of the lack of reps given to them.
For some pitchers, it can be less straightforward to make pitch adjustments in the middle of the season, but for Bassitt, whether intentional or not, this adjustment seems to be working.
Logan Gilbert
Scaling back to a more traditional FF, SL, CB, CH arsenal, Seattle Mariners’ highly-touted prospect, Logan Gilbert, has had a respectable rookie season thanks in large part to his exceptional four-seam fastball.
Gilbert’s slider has roughly league average stuff, but is his worst pitch in terms of intrinsic run values, followed closely by the curveball, which grades out poorly in terms of stuff. Despite the slider having a few inches of vertical lift on it, its velocity differential puts it in the same group as curveball velocity drops. The graph below is the same velocity-sweep tradeoff we generated for Burnes, but for Gilbert we connected the average velocity differentials for both actual and expected shapes.
In this visual, square represents the average velocity differential of the pitch, and the circle represents the average expected velocity differential. The other component is the average horizontal movement, so we must consider that the expected velocity differential (circle) is not precisely the amount of sweep we would expect the pitcher to possess.
Each of Gilbert’s breaking balls could use quite a boost in velocity; however, similar to the theme of this blog, any gain in velocity is likely to be met with changes in the amount of gloveside break. Thus, with such a large potential gain to be had, it’s possible that the shape of each pitch could change dramatically.
Individualizing a Data-Driven Pitch Design Plan
We should consider that certain pitchers can only tweak so much within their arsenal. The models we build come with that in mind, so it’s imperative to consider the athlete’s personal talent levels and historical tradeoffs before making an adjustment to a pitch.
Other tradeoffs may show up and make further decisions or reevaluations necessary.
One component we did not discuss in this blog was the tradeoff between breaking ball velocity and spin efficiency. This is something that will be covered in the second post of this series.
Pitch design is not a linear process. The beauty in designing a pitch is the trial-and-error process of exploring different possible shapes and characteristics. As outlined in Driveline’s Basics of Pitch Design certification course, trial-and-error occurs at every phase of the pitch design process, with many of these phases overlapping.
While we can determine objective measures that make pitches more effective, there is a level of individuality still involved in deciding the unique adjustments. That’s why having a model to estimate the expected velocity differentials eliminates some guesswork in determining the proper shape for a given pitcher.
In the end, a roadmap with some stones uncovered is far more appealing than one with more mysteries.
Comment section