Mastering The Axis of Rotation: A Thorough Review of Spin Axis in Three Dimensions
When we observe the trajectory of an incoming pitch as it is released from a pitcher’s hand, we inevitably witness the interaction of a pitch’s total spin, release angle, initial velocity, and axis of rotation within the environment.
We perceive all of this information simultaneously, and make a determination on the spot as to whether we think the quality of a pitch is good, average, or poor.
The simplicity of measuring pitch quality via the eye test mentioned above is likely something we take for granted, particularly when we consider how complicated things can get when we try to quantify a pitch by its individual parts, rather than the sum of the whole.
Despite this difficulty, measuring a pitch by its individual characteristics is a necessary requirement in modern pitch design sessions when we’re identifying areas of need, monitoring progress, and developing new pitches.
Many pieces have been written by analysts (and ourselves) to help overcome the questions coaches and athletes face during pitch design; however, Spin Axis, arguably one of the most important and nuanced pitch components to conceptualize, has largely been overshadowed and ignored in the public realm, relative to other pitch characteristics.
To remedy the lack of attention given to Spin Axis, we’ll attempt to address many of the misnomers and areas of confusion surrounding the metric. The goal here is to bridge the gap between what we know about a pitch’s axis of rotation and other attributes of a pitch’s trajectory.
Starting with the Basics: Looking at Spin Axis in Two Dimensions
Naming Discrepancies
Perhaps one of the most frustrating areas of confusion surrounding Spin Axis is knowing what to call it. The original definition of ‘Spin Axis’ used by MLBAM during the beginning of the PitchFx Era (2007/2008) described the term as the estimated direction of movement via spin, in degrees, in only two dimensions (more specifically, the x-z direction, or the plane perpendicular to the direction of travel).
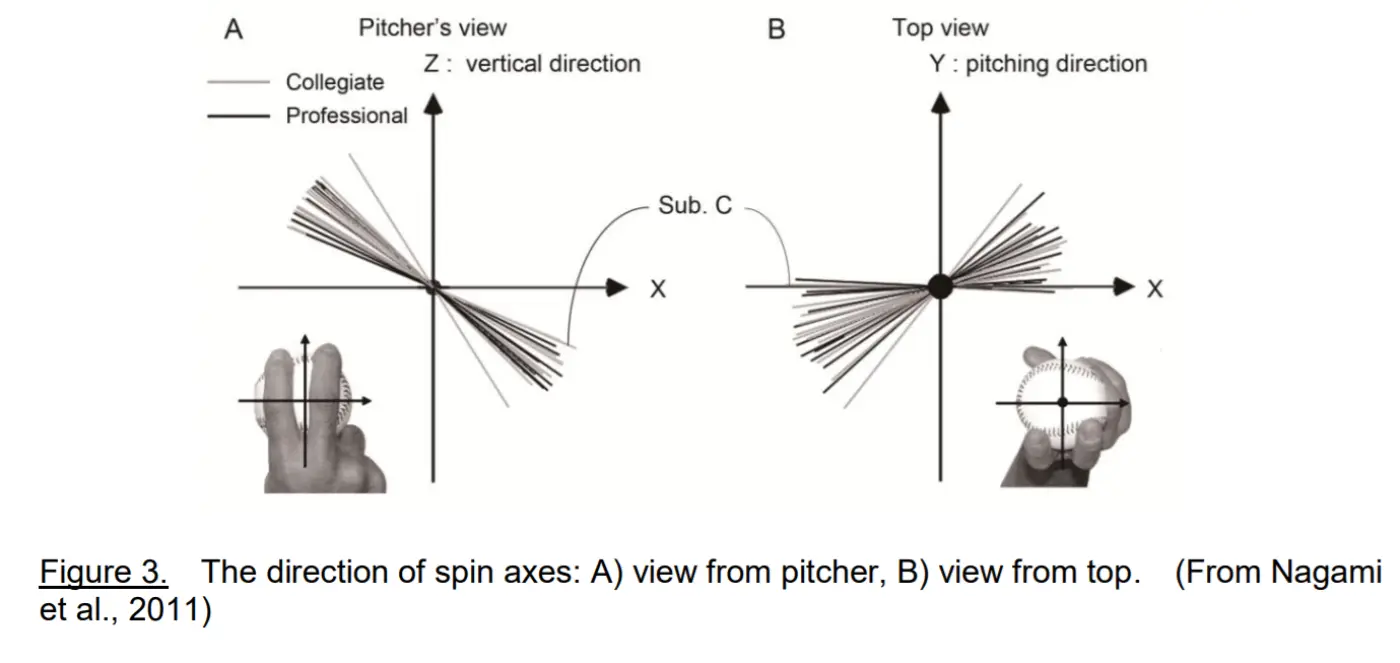
As we now know, a pitch’s axis of rotation is not defined in two dimensions; rather, Spin Axis is determined in three dimensions and is significantly correlated with the orientation of the pitcher’s hand just before ball release (Jinji, Sakurai, & Hirano, 2011).
By incorrectly defining Spin Axis as the axis of rotation in two dimensions (shown on the left in the image above from Nagami et al., 2011), many have confused the term Spin Direction—which, we argue, is the proper name for Spin Axis in two dimensions—with Spin Axis itself.
Thus, to clarify any confusion regarding the definition of Spin Axis moving forward, Spin Direction describes the axis of rotation of an incoming pitch in two dimensions (the x-z plane), whereas Spin Axis describes the axis of rotation in three dimensions (both the x-z and x-y planes).
Calculating Spin Direction
Since translating movement into degrees isn’t necessarily the most intuitive process, a neat shortcut developed by Bahill and Baldwin called the right-hand rule provides us a straightforward way to determine the Spin Direction of a given pitch without the need for advanced technology. As shown in the picture below, if one simply wraps their fingers around the direction of spin of a hypothetical pitch in the x-z direction and extends their thumb all the way out, their thumb will be pointing in the direction of the axis of rotation in the x-z plane.
(Image taken from Bahill & Baldwin, 2007)
To translate the position of this outwardly facing thumb into degrees, one can turn to the polar coordinate plot provided in the space below to find which degree coincides with where the thumb is pointing to.
In the example given in the picture above, the thumb is pointing straight up, which coincides with a 90-degree value in the polar coordinate plot and the correct Spin Direction measurement for that pitch.
If the right-hand rule is a bit too basic, there are two alternative methods you could use to find spin direction.
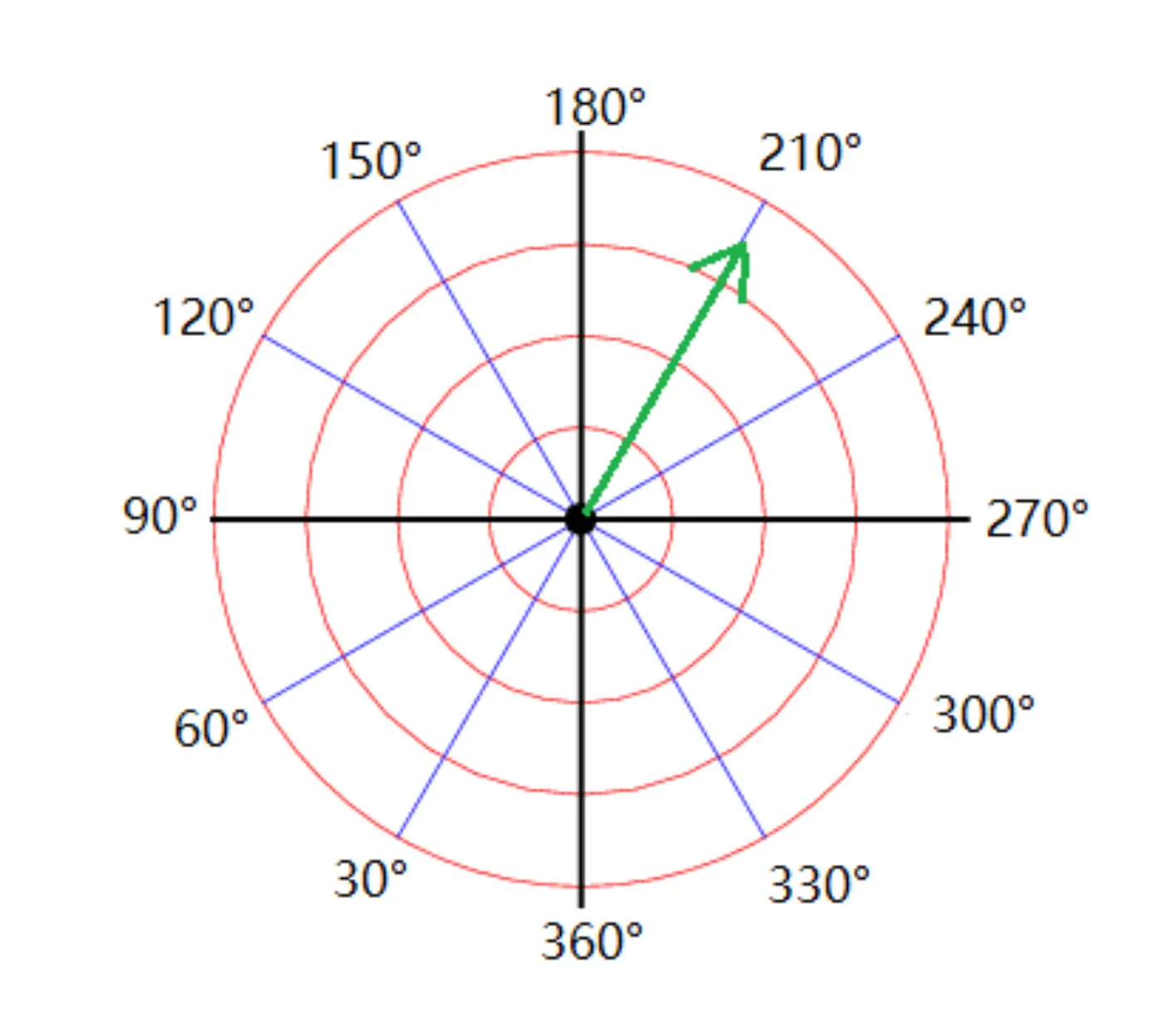
Calculating Spin Direction From the Batter’s Perspective
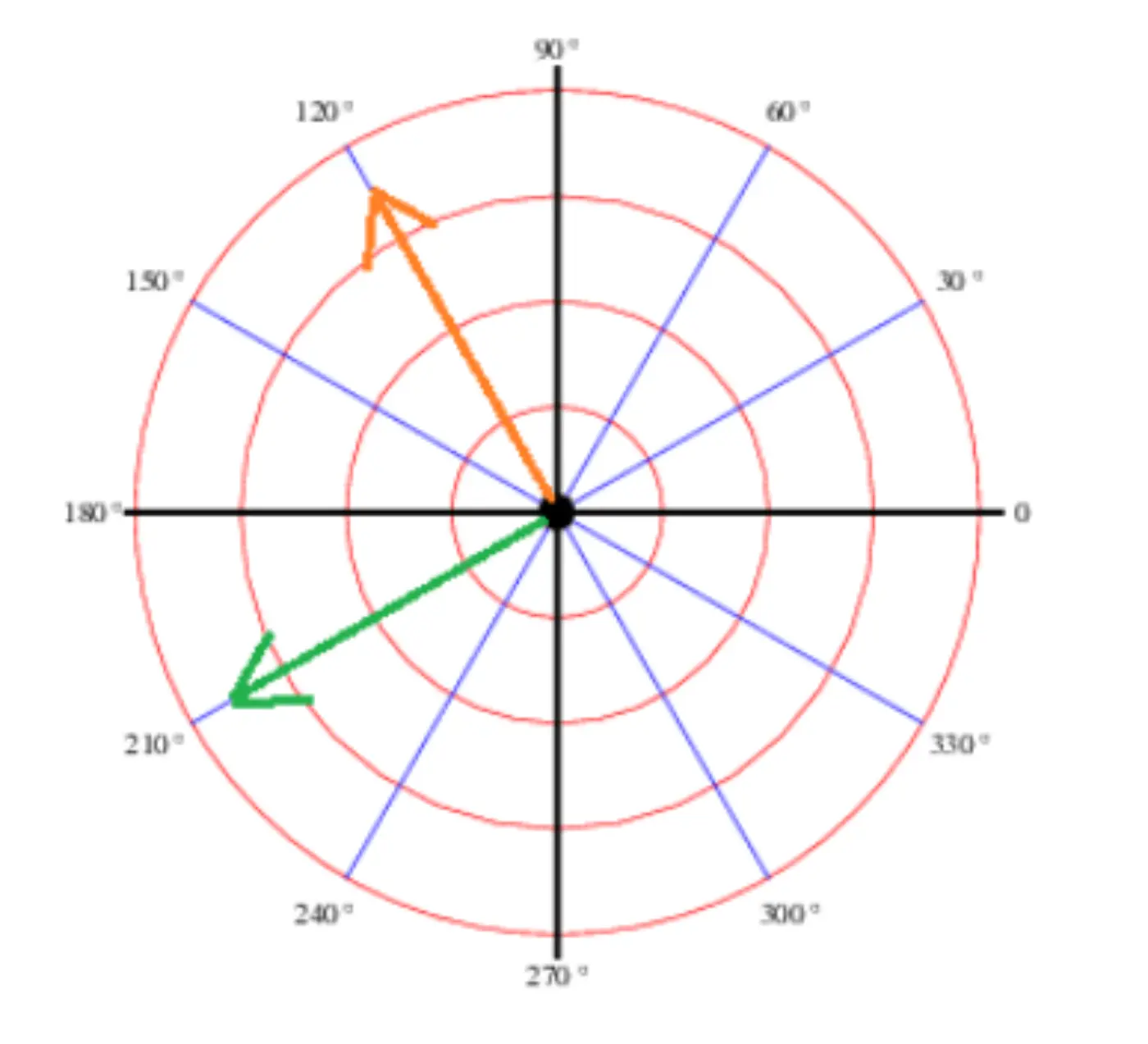
- Find the direction the ball will move from the batter’s perspective.
- Locate that direction on the polar coordinate. (For example, an average RHP’s four-seam FB will move up and to the left from a batter’s perspective. This is represented by the orange arrow pointing at 120 degrees.)
- Add 90 degrees to that value. (If we add 90 degrees to the 120 degrees found in the bullet point above, we find that the Spin Direction in question is 210 degrees. This is represented by the green arrow below.)
Calculating Spin Direction From the Pitcher’s Perspective
- Re-orient the polar coordinate so that 180 degrees is at the highest point on the circle, 90 degrees is to the left, and 270 degrees is on the right (as shown below.)
- Find the direction the ball is moving via spin from the pitcher’s perspective and line that up with the appropriate degrees. (The green line below represents a RHP’s four-seam FB.)
Spin Direction v. Tilt: What’s the Difference
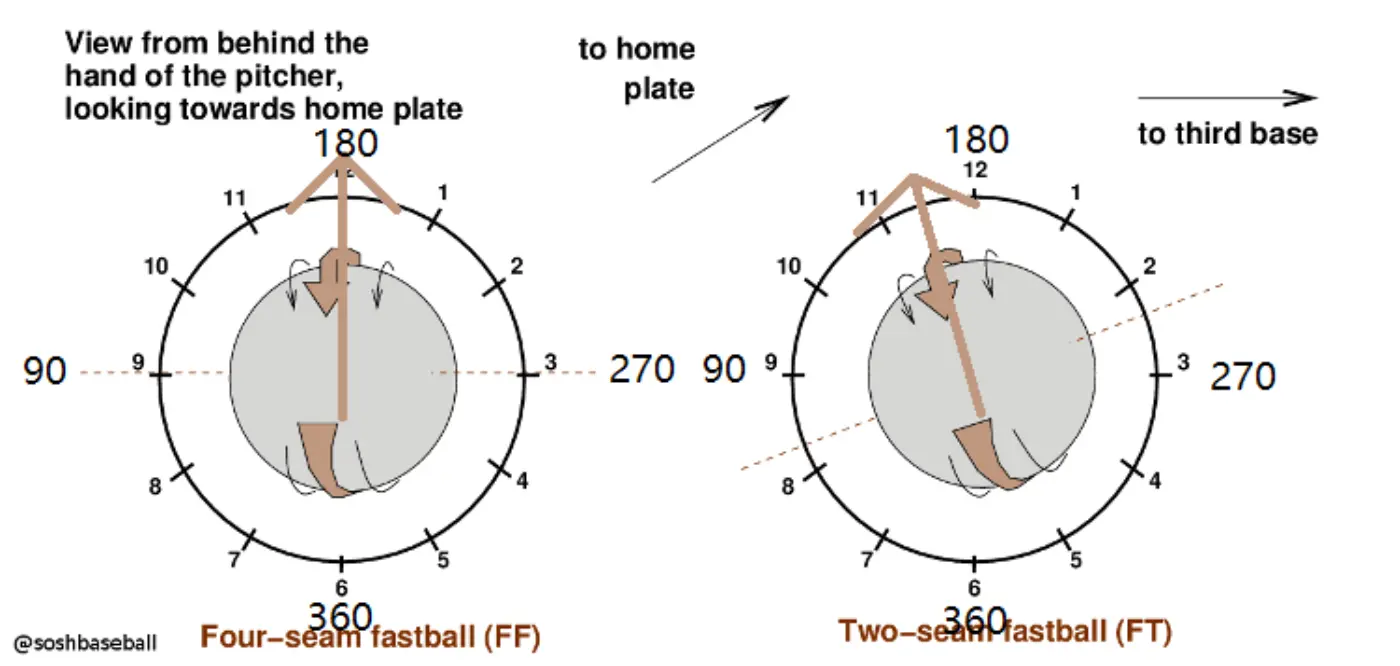
Of course, calculating a metric that references a polar coordinate is probably less than ideal for those of us who struggled with trigonometry in high school, so both Trackman and Rapsodo introduced a metric called Tilt to the baseball community. Tilt, which is just a slight derivative of Spin Direction, reports the axis of rotation in the x-z plane in units of hours and minutes instead of degrees.
By translating the polar coordinate plot so that 180 degrees = 12:00, 90 degrees = 9:00, and 270 degrees = 3:00, accurately determining a pitch’s axis of rotation in two dimensions ended up becoming much more intuitive for most people. As a result, Tilt quickly became the primary metric for coaches and players to describe Spin Direction.
(The image above [originally taken from Sons of Sam Horn] shows the Tilt and Spin Direction of a LHP’s FF and FT fastballs from the perspective of the pitcher.)
Spin Direction v. Tilt: How do they compare?
While the shift from Spin Direction to Tilt as the preferred way to report a pitch’s axis of rotation in the x-z plane has helped the metric gain popularity in the baseball community, it should not be forgotten by coaches and analysts that Spin Direction still contains value as a standalone metric as well.
For example, if you’re using a Rapsodo unit for pitch design sessions and only have access to Tilt, you’ll be unable to calculate averages on a per pitch type basis, given that the figures provided to you will be in units of hours and minutes (try plugging that into a calculator) instead of degrees.
However, if you’re aware that both Tilt and Spin Direction are calculated in the same manner, then you know that each hour of Tilt is equivalent to 30 degrees of Spin Direction (360 degrees / 12 hours = 30 degrees per hour) and each minute of Tilt is equivalent to .5 degrees of Spin Direction (360 degrees / 720 minutes = .5 degrees per minute.)
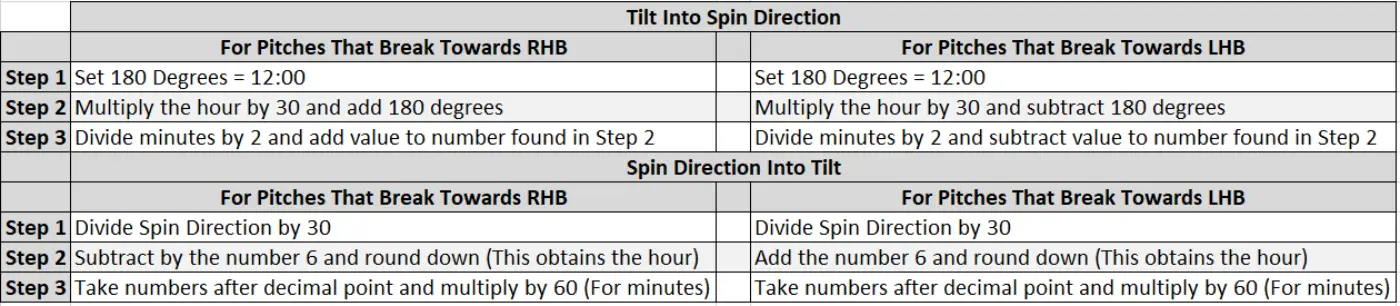
Therefore, to calculate the average Tilt for a given pitch type, all you would need to do is convert the Tilt of each pitch to Spin Direction using the formulas provided below, then find the average Spin Direction of the pitch type in degrees and convert that number back into Tilt.
(Above is a step by step guide to converting Spin Direction and Tilt. As an example, take a RHP who throws a FB at 1:10. Since that pitch broke arm side, we set 12:00 to 180 degrees, we multiply the hour (1) by 30 and add that value to 180 (210). We then take the minutes (10), divide by two (5), and then add that value to 210. Thus, our Spin Direction is 215 degrees. To convert back into Tilt, divide Spin Direction (215) by 30 (7.1667), subtract by 6 and round down to obtain the hour (1). Take the numbers after the decimal point (.1667) and multiply by 60 (10) to obtain the minutes. Our Tilt is back at 1:10.)
Thus, both Spin Direction and Tilt can work in conjunction with one another when trying to better understand a pitch type’s axis of rotation. Knowing when to use each metric to your advantage can be beneficial when working through multiple pitch design sessions with a given athlete.
Addressing Misnomers of Two Dimensional Spin Axis: Arm Slot and Spin Direction
Apart from calculating Spin Direction and Tilt, the other main area of confusion surrounding Spin Direction is how it relates to arm slot. Most coaches and players are aware that there is a relationship between Spin Direction / Tilt and arm slot, but only one prior study (Brooks, Fleisig, & Pavlidis, 2015) has explored the relationship between the two in detail.
To further investigate the relationship between Arm Slot and Spin Direction ourselves, we estimated the arm slot of every MLB pitcher from 2015-2018 using methods similar to Cross (2015) and then bucketed these pitchers by average arm slot and player season.
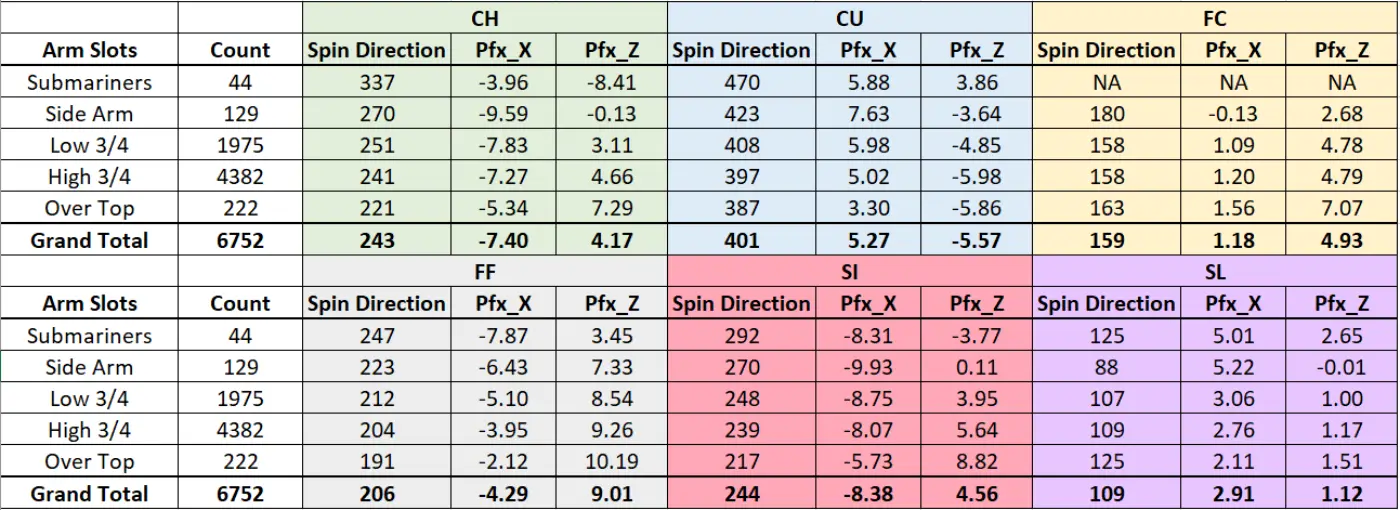
With 6,752 player seasons containing an estimated arm slot classification, we further grouped these values by pitch type to produce the table below.
(The table above shows the average Spin Direction and movement profiles of pitch types by arm slot. Note, we extend Spin Direction past 359 degrees for CBs to account for ‘backup’ CBs. With our adjustments, we find that an over-the-top pitcher’s CB has an average Spin Direction of 387 degrees, which is the equivalent of 27 degrees on a polar coordinate plot.)
For virtually every pitch type, we see that a lower slot leads to an east-west movement profile (running FBs and sweeping breaking balls), whereas a higher slot leads to a north-south movement profile (high carry FBs and 12-6 CBs).
With the help of edgertronic footage, we can see exactly why this occurs. Lower slot pitchers have a hand and wrist orientation that is more parallel to the ground relative to their high slot peers, leading to more run and sweep. On the contrary, over-the-top pitchers have a hand and wrist orientation that puts them in a position to maximize top spin or back spin, giving them more carry on the FB and 12-6 shape on the CB.
(In the images above, we see how the differences in slot between a high ¾ release point [top] and a low ¾ release point [bottom] influences Spin Direction / Tilt. The uppermost image has a Tilt of 12:40, whereas the bottom image has a Tilt of 2:06.)
The Variation Between Spin Direction and Expected Spin Direction
Clearly, there is a strong relationship between Arm Slot and Spin Direction, but the correlation between the two isn’t perfect given the mechanical and anatomical differences from pitcher to pitcher.
To investigate just how far a pitch type’s Spin Direction can be manipulated from its expected Spin Direction by arm slot, we took the seasonal averages of each MLB player’s Spin Direction by pitch type, paired that number with the expected axis of each specific pitch type given the player’s arm slot bucket, and subtracted the difference between the two.
With our new values, we were able to compare the differences in a player’s actual Spin Direction with their expected Spin Direction given their slot for each pitch type since 2015.
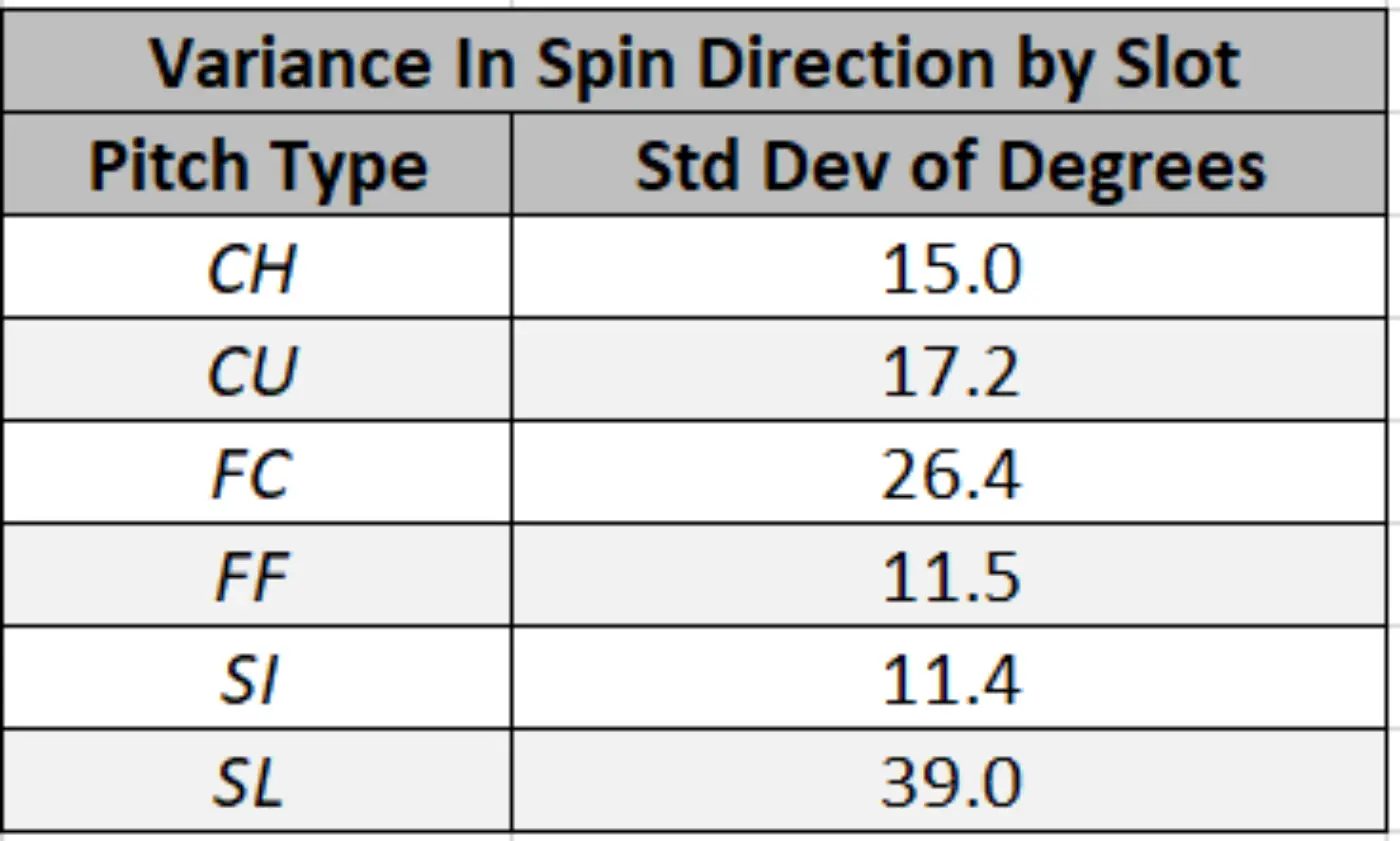
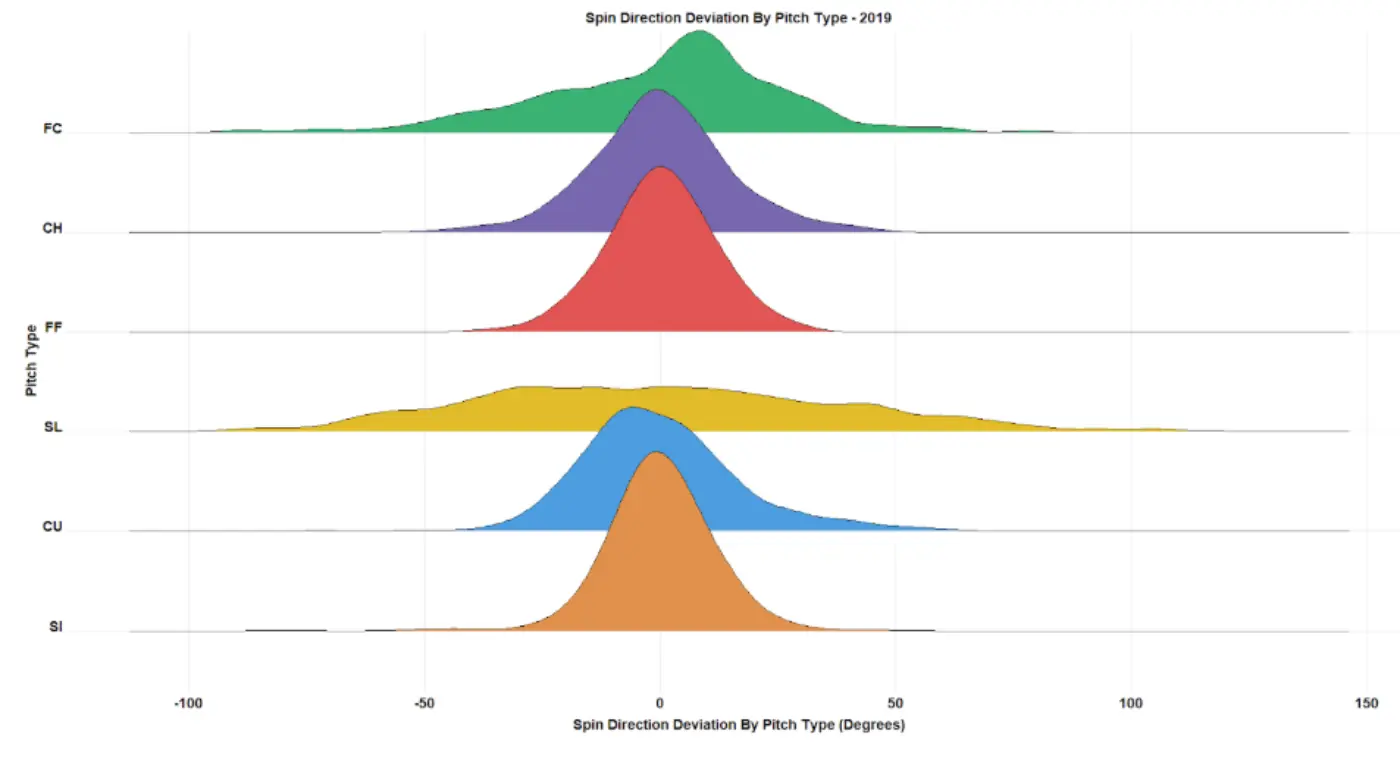
Our results indicate that MLB pitchers can add or subtract roughly 30 degrees from their expected spin direction on FBs and up to ~85 degrees on SLs (accounting for misclassifications). We feel that this is a sizeable amount of variance on a per pitch type level, lending support to the idea that pitchers can manipulate the axis of rotation on their secondary pitches without necessarily changing their release point or overhauling their mechanics.
This finding is important, as it tells us that altering the Tilt or Spin Direction of a pitch during a pitch design session can lead to significant changes in the shape of a pitch.
(The image above highlights the distribution of Spin Direction away from per-slot expectations by pitch type. Note, secondary pitches likely have inflated values due to misclassifications.)
Dissecting Gyro Components: Discussing Spin Axis in Three Dimensions
Of course, when manipulating a pitcher’s axis of rotation on a given pitch type, Spin Direction / Tilt is only one of two metrics that needs to be considered. As mentioned earlier, Spin Axis is a three-dimensional concept, which moves along an x-y axis (or gyro component) as well.
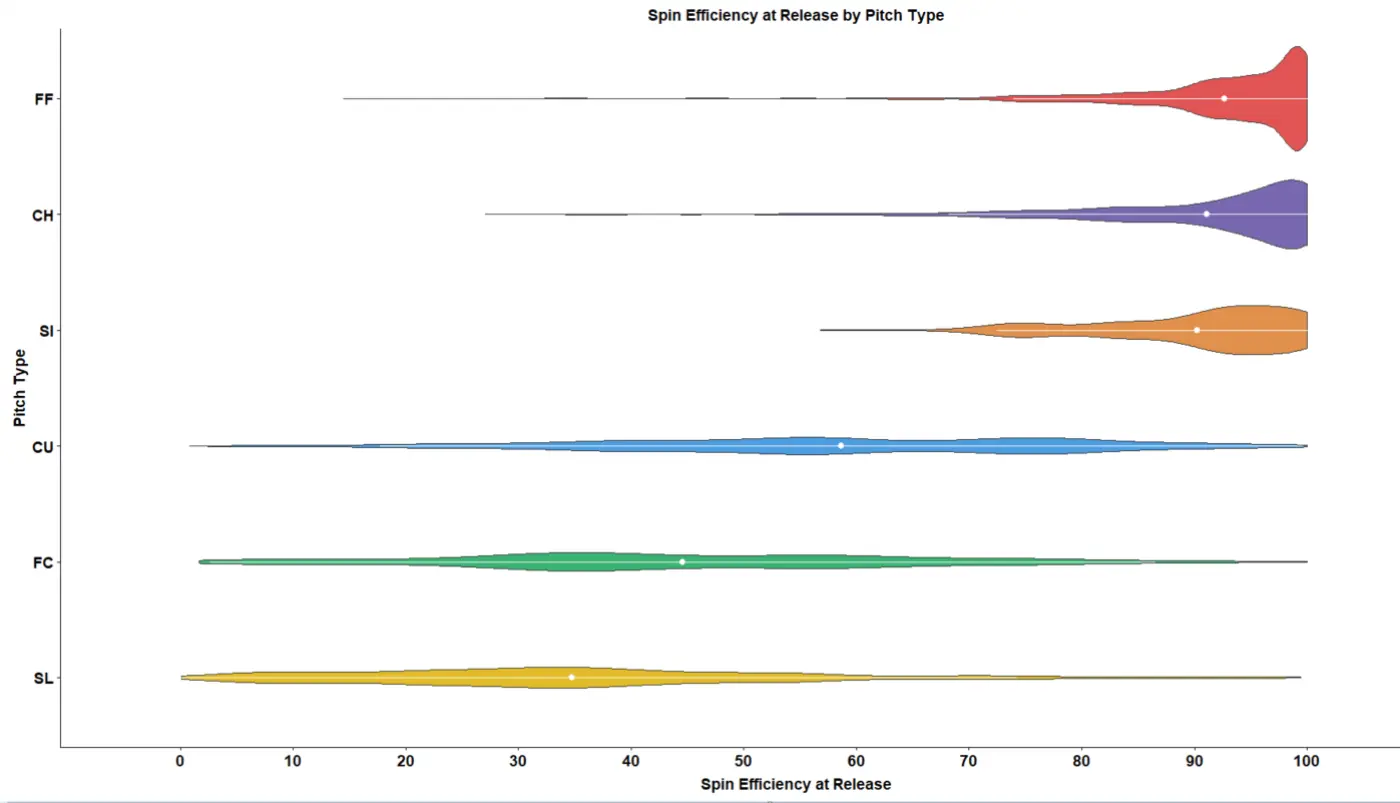
Typically, the x-y component of a pitch’s axis of rotation is represented in units of Spin Efficiency or Active Spin, which is defined as the percentage of spin directly impacting the movement of a pitch (Rapsodo).
(The image above shows the distribution of Spin Efficiency at release for each pitch type in our Rapsodo database.)
In more technical terms, Spin Efficiency divides the proportion of a pitch’s spin components in the x and z direction (the square root of the sum of side spin and back spin) by the total spin imparted on the baseball.
Given that spin in the x-z direction (transverse spin) directly influences movement, whereas spin in the x-y direction (gyro spin) does not, Spin Efficiency is used by coaches and players to determine what percentage of spin imparted on the ball is causing it to move, as well as how the spin axis of the pitch is oriented in the x-y direction (towards home plate.)
Like Tilt, Spin Efficiency is an extremely effective metric because of its intuitive nature; however, it does have limitations in describing a pitch’s axis of rotation that are important to be aware of.
Limitations of Spin Efficiency
For one, Spin Efficiency does not provide any information to players and coaches about what the relationship is between a pitch’s axis of rotation in the x-y plane and movement. As a result, many coaches and players mistakenly assume, for example, that the relationship between Spin Axis and Spin Efficiency is linear and that a pitch with 50% Spin Efficiency has a Spin Axis that is directly split in-between being perfectly perpendicular and parallel with the direction of travel.
(Spin Efficiency is the cosine of Gyro Degree multiplied by 100. As a result, a Spin Axis with a 45 degree axis of rotation in the xy plane will not have 50% Spin Efficiency)
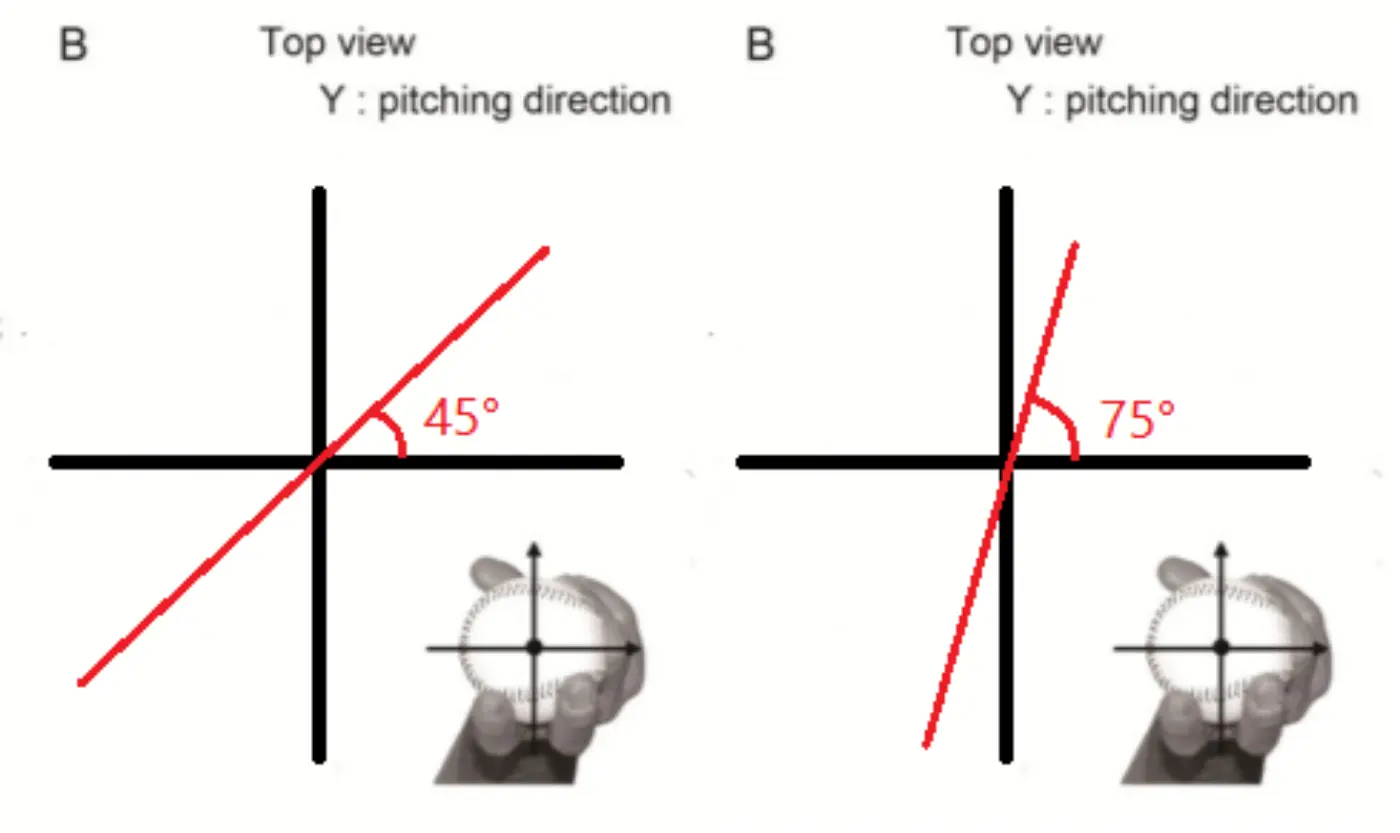
Unfortunately, Spin Efficiency does not have a linear relationship with Spin Axis in the direction of home plate (it’s actually calculated by taking the cosine of the angle that the spin axis of a pitch makes with the xz plane), which is why we prefer the metric Gyro Degree (defined in the image below) as a more descriptive and accurate measurement of the true Spin Axis of a pitch .
(Above, we see how Gyro Degree is calculated for two pitches from the overhead perspective. Pitch #1 [on the left] has a Gyro Degree of 45 degrees which is perfectly in between pure gyro spin (90 degrees) and pure transverse spin (0 degrees). The Spin Efficiency on this pitch is ~71%. Pitch #2 [on the right] has a strong gyro element to its axis of rotation, demonstrated by the 75 degree Gyro Degree. This pitch has a Spin Efficiency of ~26% [Image doctored from Nagami et al, 2011].)
Given the unique relationship between Gyro Degree and Spin Efficiency, most coaches and players are unaware of how the two relate to one another in terms of movement. As shown below, this has important implications when developing or evaluating a pitch type offering.
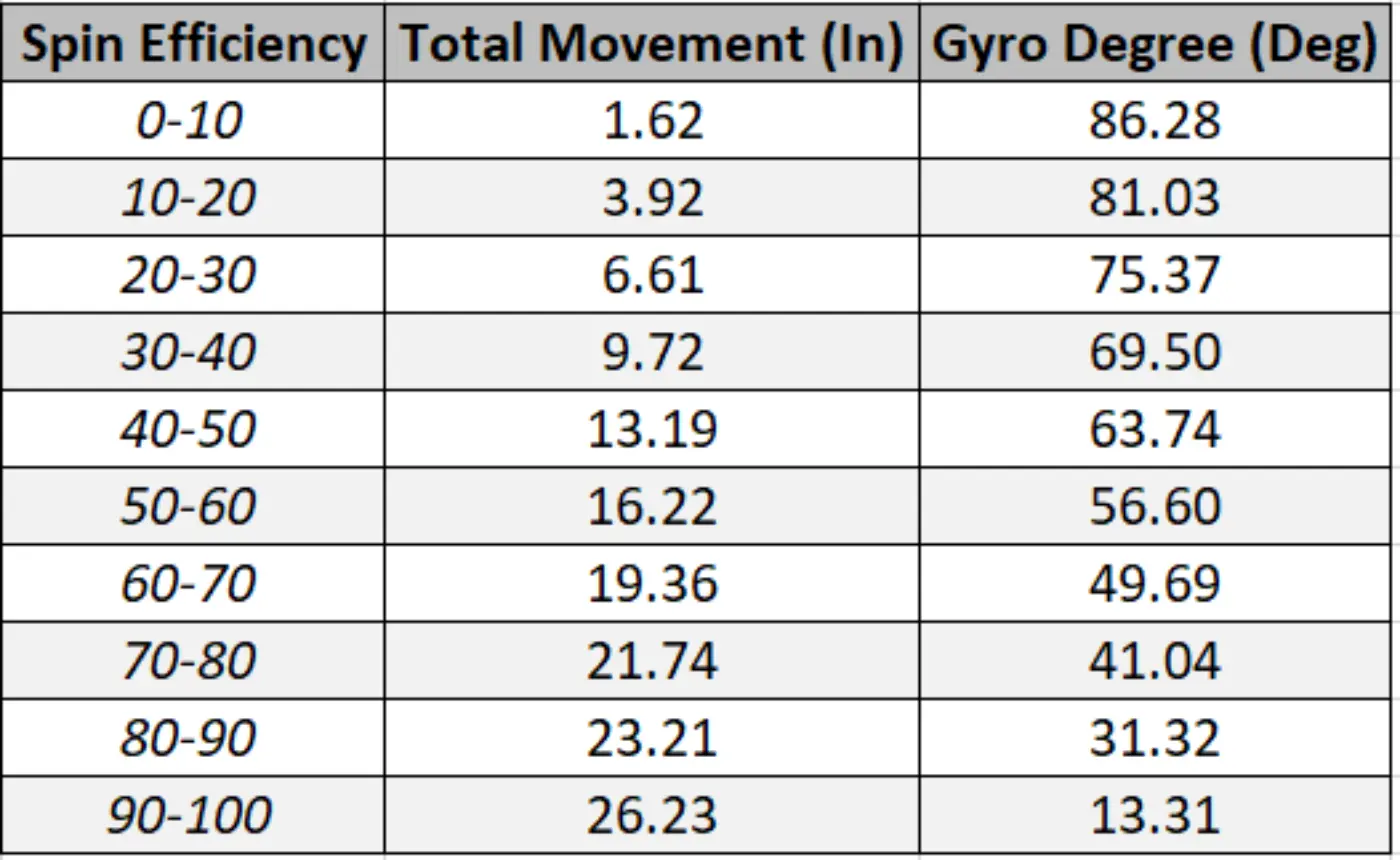
(The change in total absolute movement and Gyro Degree by increments of 10% Spin Efficiency. RHP only.)
Since cosine is more sensitive to changes at ~90 degrees than ~0 degrees, we see that players who throw a Gyroball would only need to adjust their Gyro Degree by ~11 degrees to gain ~20% efficiency, while players throwing a Fastball with 70% efficiency would need to adjust their gyro degree by ~28 degrees to increase their efficiency by the same amount.
The key takeaway here is that gyro-heavy pitches such as CTs and SLs should be easier to add Spin Efficiency to given the sensitive nature of Spin Efficiency at that level of Gyro Degree. Further, gyro-heavy pitch types will also have more volatile Spin Efficiency readings (a slight deviation in spin axis can have a large impact on Spin Efficiency) on a per pitch basis for the very same reason.
A Negative Gyro Degree vs. A Positive Gyro Degree
Another slight issue with Spin Efficiency is that it is indifferent to whether the Gyro Degree of a pitch is pointing in a positive or negative direction relative to home plate. While this is a non-issue for most pitches (LHPs typically spin the ball with a negative Gyro Degree, whereas RHPs typically spin the ball with a positive Gyro Degree), roughly 8% of all pitches thrown will have a Gyro Degree in the opposite direction of expectation given a pitcher’s handedness.
In particular, low slot pitchers will frequently reverse the Gyro Degree on their SIs and CHs, as shown in the edgertronic footage below.
While this can be difficult to pick up at first without watermarks, our Driveline Edge tools are specifically designed to help us conceptualize the difference between two pitches with mirroring Gyro Degrees fairly easily.
(These two pitches have the same Spin Direction and Spin Efficiency, but opposite Gyro Degrees of 29.31 degrees [left] and -29.31 degrees [right].)
Gyro Spin and Movement
You might be asking yourself why the directionality of Gyro Degree matters, particularly when it’s understood that only Spin Efficiency, Spin Direction, and Total Spin determine how a pitch moves (minus drag).
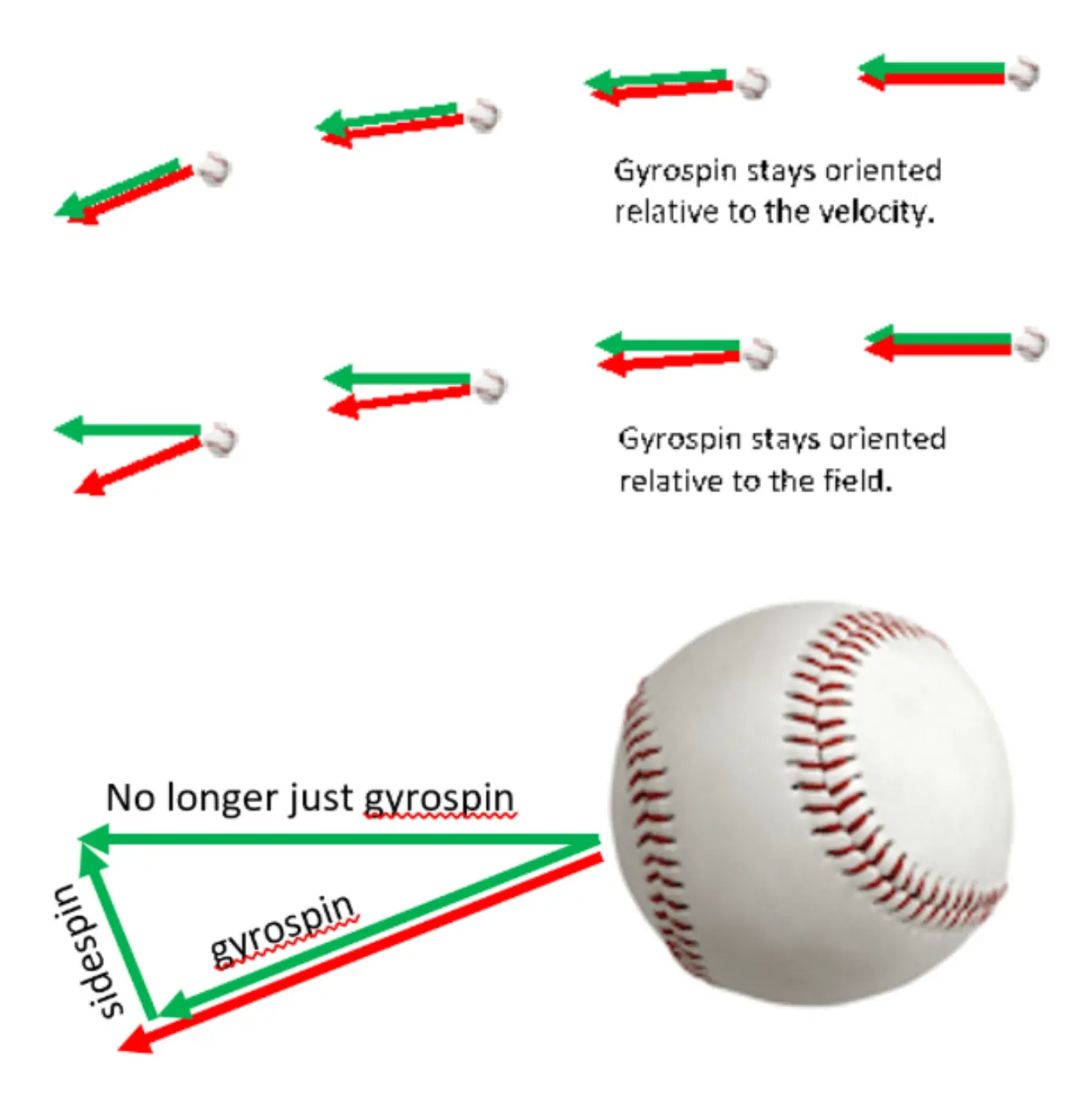
Well, unlike what most players and coaches have been taught, gyro spin can contribute to the movement of a pitch depending on the pitch’s trajectory, the amount of gyro spin it has, and which direction the Gyro Degree is pointed to.
To briefly explain, because gyro spin (and all components of spin) stays oriented to the initial velocity vector rather than the actual trajectory of the pitch itself (which is manipulated by gravity and the magnus effect), some portion of gyro spin can be turned into side spin during ball flight, while some portion of side spin can become gyro spin during ball flight.
(The top image demonstrates what would need to happen for Spin Efficiency to remain constant throughout ball flight [the green gyro spin vector maintains alignment with the pitch’s red trajectory vector.] The middle image demonstrates what actually occurs due to gravity and release angle. This separation between gyro spin and trajectory causes a change in Spin Efficiency over ball flight, as shown in the bottom image [all taken from Kagan, 2017].)
For pitches that move glove side (Sliders & Curveballs), a small amount of Spin Efficiency is typically added during ball flight by the time it reaches the strike zone. For pitches that move arm side, a small amount of Spin Efficiency is typically lost by the time it reaches the strike zone.
(As Rapsodo is optical-based, whereas Trackman and FlightScope are radar-based, Rapsodo 2.0 is able to directly measure Spin Axis and provide us with Spin Efficiency at both ball release and plate crossing. The average change in Spin Efficiency throughout ball flight is given above.)
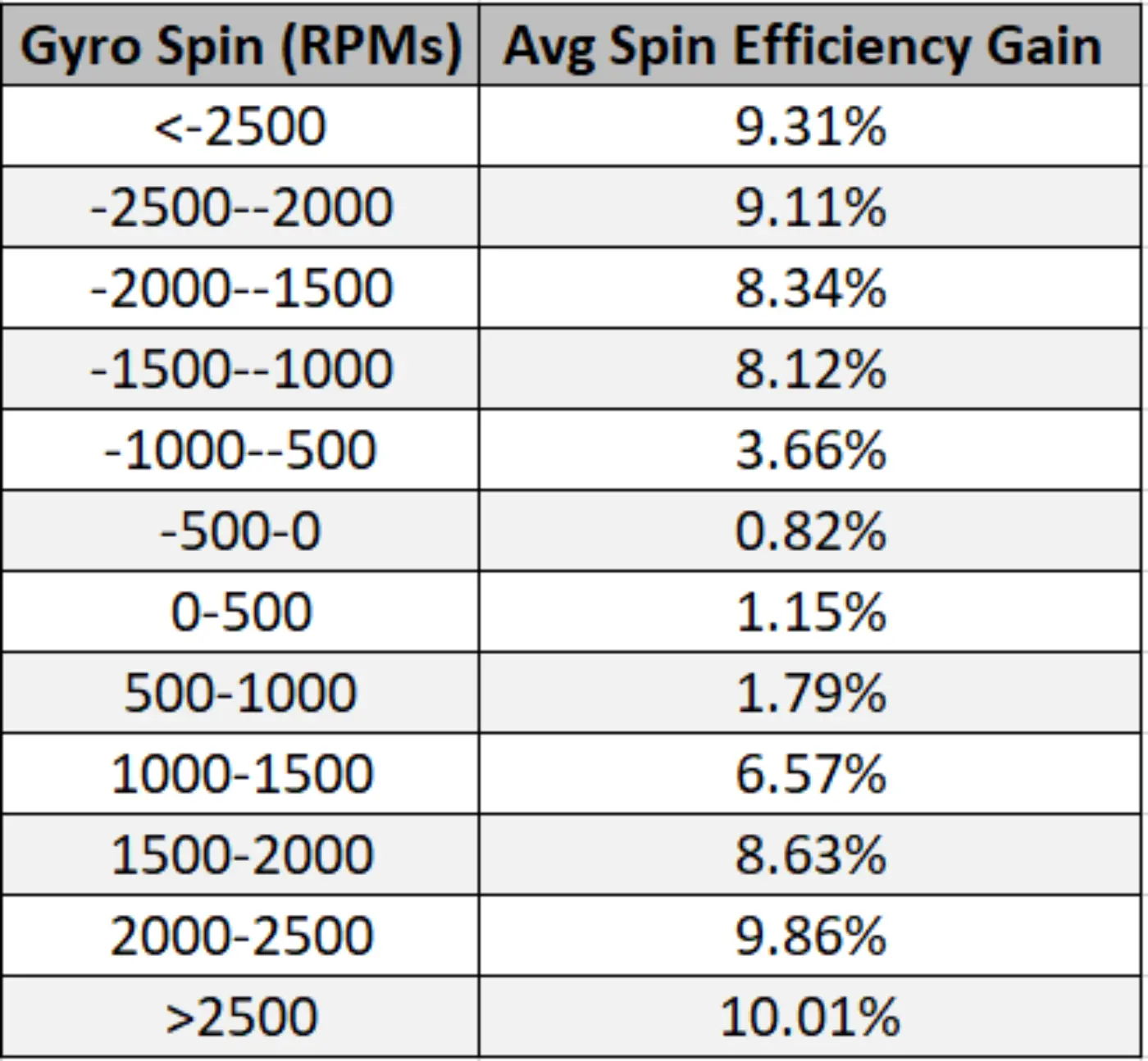
To gain a better sense of the magnitude of this effect, we bucketed breaking balls in 500 RPM intervals of gyro spin and calculated the increase in Spin Efficiency throughout ball flight.
In looking at the table below, we see that breaking balls thrown with at least 1,500 RPMs of gyro spin added ~8-10% of Spin Efficiency during ball flight, while breaking balls with less than 500 RPMs of gyro spin added just ~1% of Spin Efficiency during ball flight.
(The gain in Spin Efficiency during ball flight for breaking balls based on the amount of gyro spin they possess at release point.)
The effect size here is relatively small in terms of movement, as the change in Spin Efficiency equates to roughly 1-2 inches of horizontal break throughout the duration of ball flight. However, the key thing to note is that, in theory, this movement would occur “late” in a pitch’s trajectory. Therefore, these additional 1-2 inches of movement may be more difficult for the batter to perceive relative to more traditional movement. With a switch to an optical tracking system in MLB next season, we’ll be able to better determine whether this “late break” has additional value worth monitoring.
Back to A Negative Gyro Degree vs. A Positive Gyro Degree
With these findings in mind, we hypothesized that if FBs and CHs typically lose Spin Efficiency during ball flight, they could, in theory, gain Spin Efficiency during ball flight if they were thrown with an inverse gyro degree. Depending on the effect size, this could give a slight advantage to certain low-slot pitchers who are able to manipulate the direction of gyro spin imparted on the ball.
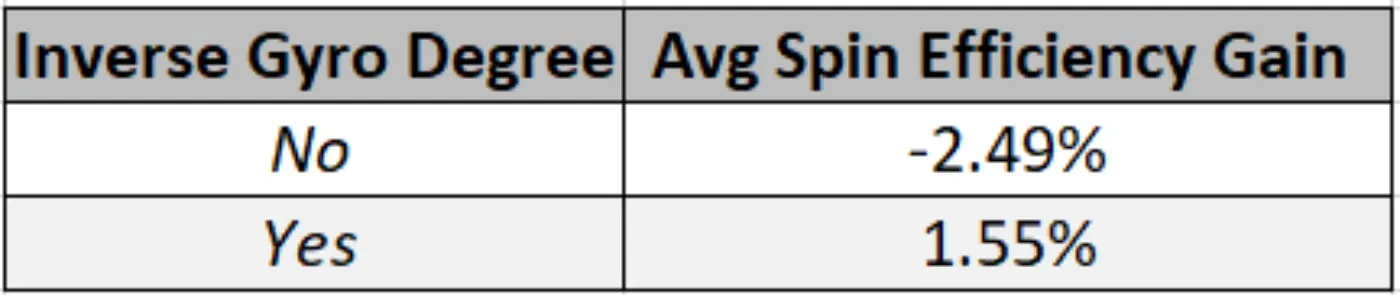
To test this, we separated all inverse Gyro Degree FBs and CHs from normal Gyro Degree FBs and CHs and averaged the change in Spin Efficiency from release to home plate for both groups. As shown in the table below, FBs and CHs thrown with an inverse Gyro Degree in our dataset gained ~1.5% of Spin Efficiency during ball flight, while FBs and CHs thrown with an expected Gyro Degree lost 2.5% of Spin Efficiency during ball flight.
Given that the effect size between the two groupings of pitches only amounts to a ~4% difference in Spin Efficiency (worth ~1 inch of movement), it’s unlikely that manipulating the direction of gyro spin influences batter perception.
However, knowing when and how an athlete produces an inverse Gyro Degree on a specific pitch may be important when trying to develop consistency with a FB or CH. Thus, monitoring inverse Gyro Degree pitches may be worthwhile if you have the requisite technology.
Comparing Spin Efficiency to Gyro Degree
To wrap up Spin Axis in the x-y plane, we believe that both Gyro Degree and Spin Efficiency serve a unique purpose in the pitch design process and are best used interchangeably with one another (similar to Tilt and Spin Direction). While Spin Efficiency is easier to conceptualize and translate to coaches and athletes, Gyro Degree is more descriptive of the actual axis imparted on the ball itself.
Putting It All Together
As you’ve probably gathered from reading this, analyzing the axis of rotation on a given pitch and putting it into proper context is both challenging and rewarding.
Since every pitch component makes up an important piece of the puzzle when designing a pitch for an athlete, it is critical that we understand how each pitch characteristic fits in with one another to put our athletes in the best position to succeed.
Spin axis is no different, and being able to more efficiently derive meaning and make adjustments to a pitch’s axis of rotation during the pitch design process can be a difference-maker when developing the right pitch.
This article was written by Dan Aucoin, Research Analyst.
Much love to Anthony Brady, John Scheffey, Alex Caravan, Michael O’Connell, and Eric Jagers for their help with this piece.
Polar Coordinate Visuals Courtesy of Wikipedia and MathWorld; Cosine Visualization Courtesy of MathIsFun.


Comment section