Computed Muscle Control Analysis of Pitching Mechanics
Continuing with our validation of a Forward Dynamic analysis of the pitching motion from last week (Part One), we had run through the initial stages of the simulation pipeline to have an accurately scaled model that is tracking the recorded kinematic motion and associated force plate kinetics closely. We are now ready to run a Computed Muscle Control algorithm in OpenSIM to calculate the specific muscle activations and forces which best reproduce the arm’s motion in order to determine how they affect the overall valgus torque imposed on the elbow.

(This article was written by Matthew Wagshol, Biomechanist in the R&D Department of Driveline Baseball.)
Individual Muscle Contributions
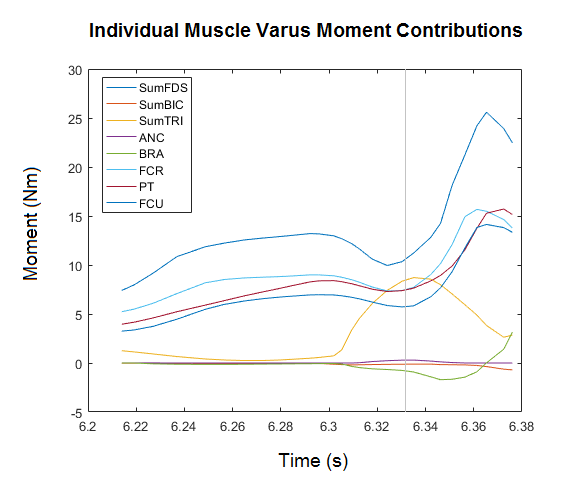
A standard muscle set is first used to determine a baseline for muscle behavior. Fourteen muscles and subcompartments were measured that cross the medial side of the elbow which can contribute a varus torque to counter the overall valgus moment at the elbow. These muscles were the Flexor Digitorum Superficialis (four compartments), Pronator Teres, Flexor Carpi Radialis, Flexor Carpi Ulnaris, Biceps (two compartments), Triceps (three compartments), Anconeous, and Brachialis.
The muscles are scaled along with the model and have been confirmed to represent the attributes of a 50th percentile male. These parameters include maximum isometric force, slack length, and stiffness (1).
The CMC process runs a weighted optimization that is set to focus on the muscles of the upper arm. Control constraints are also added to better align muscle firings with recorded EMG activity during pitching (2). The algorithm returns individual muscle forces during the motion which are then multiplied by their respective moment arms to calculate the Varus moments of each muscle compartment.
Our results agreed with those of Dr. Buffi (3) and show that several muscles produce significant Varus moments during the pitching motion. The FDS has the largest moment which peaks slightly after the maximum valgus load, along with the FCR, FCU and PT. We also saw a peak TRI moment at the time of maximum valgus load, although in our model the maximum moment was lower than that seen in the original paper. We also saw a smaller effect from the BRA and ANC, which we believe aligns better with the small moment arms associated with these muscles. These differences can be attributed to minor alterations in model definitions, but the overall trends and peak muscle contributions confirm that our Forward Dynamic framework approach is consistent with the reviewed research.
Adapted Muscle Set
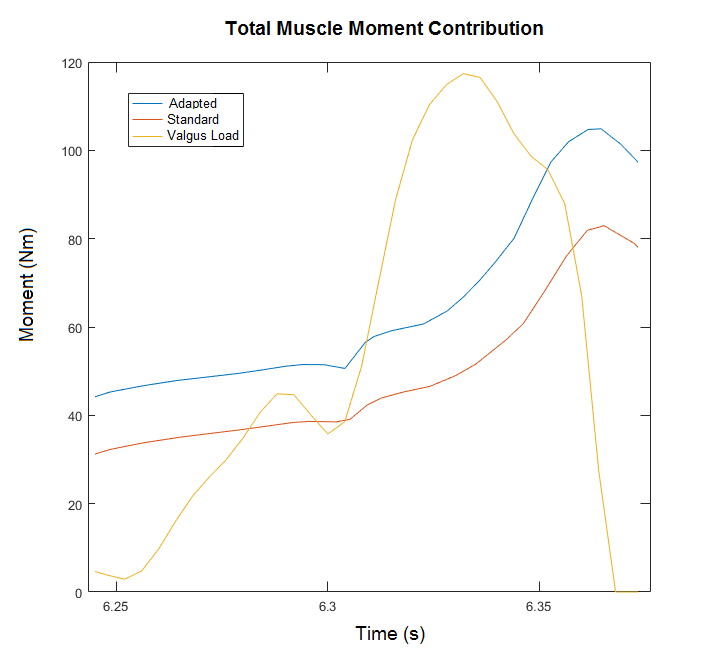
While the previous muscle contributions results are a good baseline measure, elite baseball pitcher’s have muscles that are likely significantly stronger and more powerful than an average male. To explore this idea, an adapted muscle set is defined for athletes (3) which increased the maximum isometric strength by 29%, stiffness by 70%, and decreased activation times to 0.005s.
The adapted muscles have an increased total moment contribution over the pitching motion, but we have to take some additional steps in order to fully understand how the muscles affect the load felt by the UCL. We can accomplish this by defining a biomechanical force balance at the elbow with an equation that can be used to break down the different torque contributions.
Torque Analysis at Elbow
Following Dr. Buffi’s dissertation (3), we state that the total measured valgus moment from the motion (Mvalgus) is equal to the sum of three varus moments. These varus moments are the total individual muscle contributions (Mmc), the osseous articulation moment from joint compression (Mart), and the remaining torque on the UCL (Mucl).
Therefore rearranging the equation we have:
We already know the total Valgus moment from the inverse dynamic analysis and we also know the sum of the individual muscle contribution moments from CMC. We now have to define and calculate Mart by looking at the joint compression force.
Joint Compression Force and UCL Load
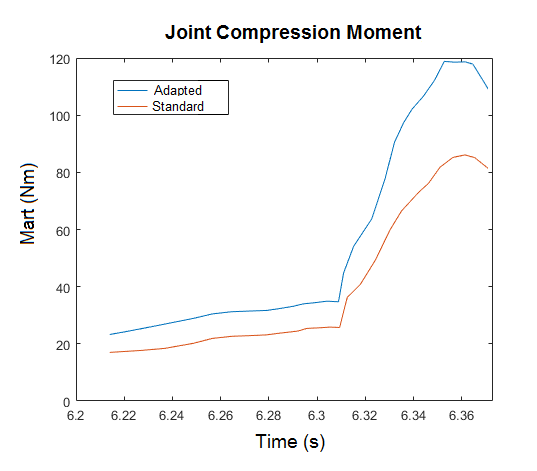
The osseous articulation moment, Mart can be defined as the joint compression force Fjc at the elbow multiplied by the corresponding moment arm dart.
Using the analysis tool in OpenSIM we are able to see the joint compression forces at the elbow over the motion. These forces are normalized to run along the longitudinal axis of the radius and be perpendicular to the varus–valgus DOF axis. We then multiply this resulting vector by dart which is defined to be the distance between the center of pressure of the osseous compression and the elbow joint center.
With Mart calculated, we can complete our equation and determine the resulting load imposed upon the UCL.
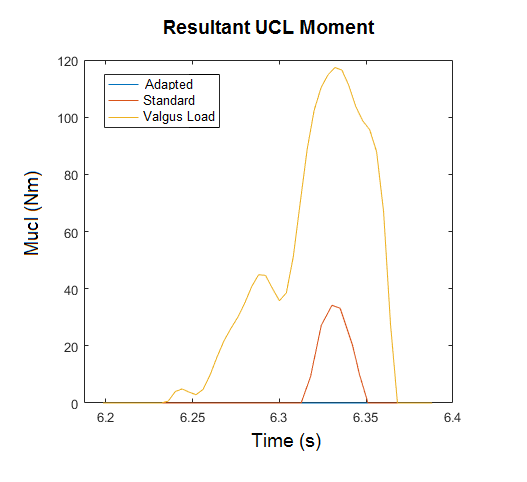
These results show that the traditional analysis of the imposed valgus load on the UCL is largely offset by muscle contributions and the joint compression force. Without muscles, the UCL would absorb all of the load, which is much higher than its carrying capacity (5). With a standard muscle set of an average male, the UCL load is greatly reduced to a peak of about 35 Nm, which is still enough torque to be responsible for injury. However, with adapted high performing muscles, the load on the UCL is reduced to 0, which means that the varus moments produced by the muscles and the corresponding joint compression force are completely countering the imposed valgus load.
Looking Ahead
These results are significant by providing a more detailed look at how individual muscles in a pitcher’s arm affect the distribution of the overall peak valgus torque from the motion. The simulation makes it clear that muscles in the arm provide a significant reduction in torque felt at the UCL, and that by strengthening these muscles to a higher level, the risk of injury can be diminished.
With this simulation framework validated, we are excited to use Forward Dynamic analysis as a tool to determine ways to improve muscle function as a pathway to reduce injury while still allowing for variation in a pitcher’s unique motion. We also intend to study the elite pitchers at Driveline Baseball to better our understanding of the adapted muscle set for athletes and fine-tune our guidelines and training protocols to ensure our pitcher’s are improving safely and effectively.
Sources:
1) Millard, M., T. Uchida, A. Seth, and S. L. Delp. Flexing computational muscle: modeling and simulation of musculotendon dynamics. J. Biomech. Eng.-T. ASME. 135:021005, 2013.
2) Hamilton, C. D., R. E. Glousman, F. W. Jobe, J. Brault, M. Pink, and J. Perry. Dynamic stability of the elbow: electromyographic analysis of the flexor pronator group and the extensor group in pitchers with valgus instability. J. Shoulder Elb. Surg. 5:347–354, 1996.
3) James H. Buffi, Katie Werner, Tom Kepple, and Wendy M. Murray, Computing muscle, ligament, and osseous contributions to the elbow varus moment during baseball pitching Ann Biomed Eng. 2015 Feb;43(2):404-15
4) Hortobagyi, T., and F. I. Katch. Eccentric and concentric torque–velocity relationships during arm flexion and extension—influence of strength level. Eur. J. Appl. Physiol. O. 60:395–401, 1990.
5) McGraw, M. A., T. E. Kremchek, T. R. Hooks, and C. Papangelou. Biomechanical evaluation of the docking plus ulnar collateral ligament reconstruction technique compared with the docking technique. Am. J. Sports Med. 41:313–320, 2013.
Comment section