Pairing Blast and Hittrax Data Part 2: Specific Focuses
In our last piece, we took a surface level look at the first publicly available pairing of Blast and HitTrax data. In this piece, we take a look at commonly held, specific beliefs that have been touched upon by our hitting trainers and see whether the data backs it up. We also take a more nuanced view of a popular sabermetric proxy for evaluating attack angle via unsupervised learning.
Since our last post, we’ve added over 2000 sample swings of paired HitTrax and Blast data.
This piece includes a very granular examination of some very specific contentions, so to save time, here are the direct theses we are examining:
- Contention A: Hitters with higher early connection degrees in the top of the zone have less productive BBEs (Batted Ball events).
- Contention B: Athletes likely have high EV on pitches in the lower third of the zone and low EV on pitches in the top third of the zone (for connection_at_impact > 100).
- Contention C: Athletes take too long to reach peak rotational speed during swing and will likely struggle to achieve high EV at deeper points of contact (for rotational_acceleration_<15).
- Contention D: The 1/8th rule average LA makes for a suitable proxy for attack angle on a macro scale (per hitter). (More detail below but on exploring methods for reverse engineering attack angles.)
One final disclaimer: these findings are meant to be purely numerical with robust statistical merit rather than any sort of coaching indicator or lesson. The first three contentions are commonly believed both internally and among other analytically minded hitting instructors, and so now is the time to assess these claims.
A few quick definitions of the Blast metrics we discuss in this piece are necessary for comprehension:
- Early connection is measured in degrees as the relationship between body tilt and vertical bat angle (the angle of the barrel of the bat relative to the knob of the bat at impact) at the start of the downswing.
- Connection at impact measures the same relationship as early connection but at impact instead of the start of the downswing.
- Rotational acceleration is measured as the speed with which the bat accelerates into the swing plane.
- Attack angle is measured as the angle of the bat’s path at impact, relative to horizontal with a positive value indicating swinging up.
Ok, with a few disclaimers and definitions out of the way, let’s roll up our sleeves.
Contention A
Contention A has already been touched upon in the public Twittersphere.
Fires me up when @maxgordon40 hits me up with a theory about Early Connection Deg (Blast metric) and fires me up even more when his theory is validated by d@tA.
Gordo proposes that hitters with higher early connection deg’s in the top of the zone might have less productive BBEs pic.twitter.com/nAf4QNtW1k
— Alex Caravan (@Alex_Caravan) March 7, 2019
To touch back on this, this contention seems largely true. The mean early-connection figure for HHB or Hard-Hit Balls (measured here as EV over 90) is a little lower than for the non-HHB population for swings both in the bottom and top of the zone. So if anything, we can extend the contention to hold true for the rest of the zone, keeping in mind that the sweet spots are relative: What’s too high of an early-connection degree in the bottom of the zone is of greater money value in the top of the zone.
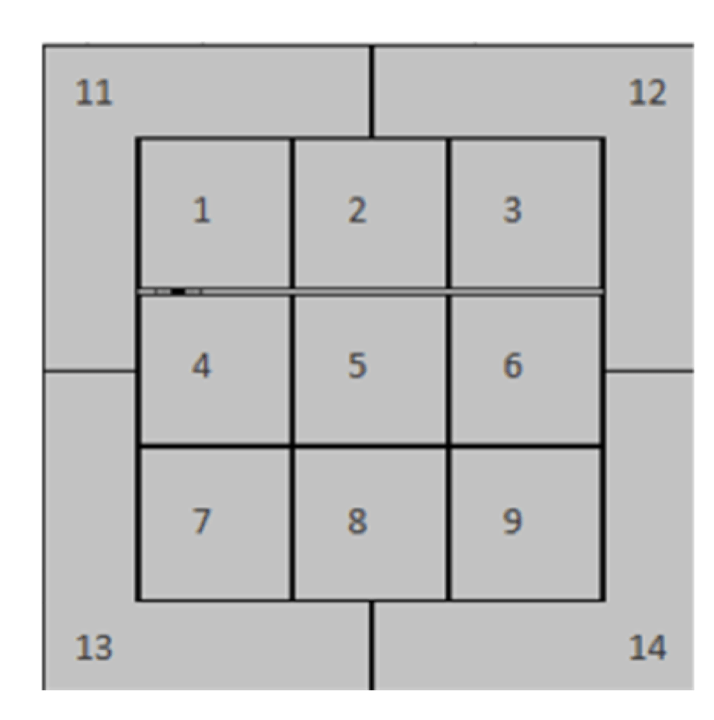
As a side note, the top and bottom of the zone was split up accordingly and depicted below:
- The top of the zone includes the 1, 2, 3, 11, 12 split-out zones.
- The rest of the zones are in the same vein.
The zone was additionally calibrated for each hitter’s height and stance, per HitTrax.
Contention B
Athletes likely have high EV on pitches in the lower third of the zone and low EV on pitches in the top third of the zone (for connection_at_impact > 100).
First off, the similar scope of this question prompts us to recycle the same graphic.
So using the same top and bottom of the zone denotations, we now look at the kernel density (a smoothed depiction of a random variable’s probability density function, or just a fancy way to show where most of the variable’s values lie) of exit velocity (rather than investigating the swing-characteristic metric of early connection as we did in the previous contention) and split up our large data frame into four main subgroups:
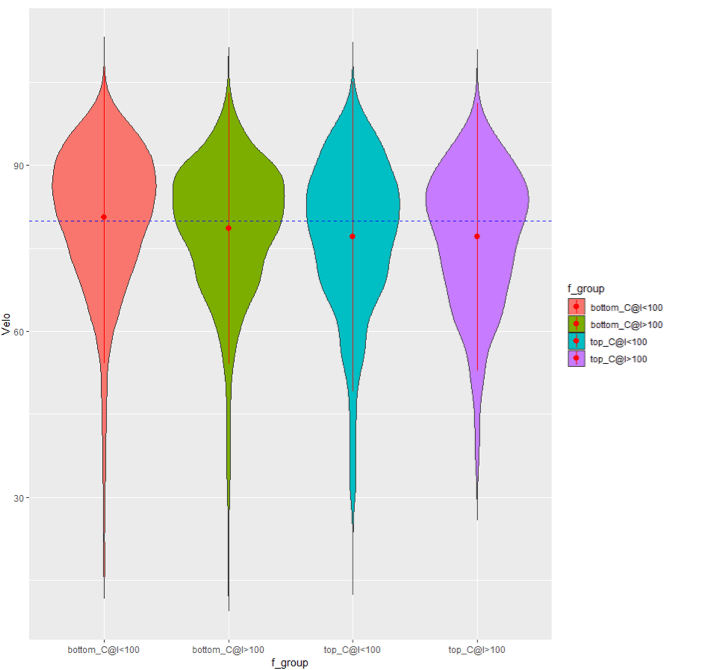
| Zone | Connection @ Impact Deg | Mean EV |
| Top | >= 100 | 78.58 |
| Top | <100 | 80.62 |
| Bottom | >= 100 | 77.09 |
| Bottom | <100 | 77.11 |
It looks like there is a ~1.5 mph EV difference between the top and bottom of the zone when the connection at impact is above 100, but it looks like the gap widens when looking at the swing metrics under 100 degrees. In fact, when running a within-subject, one-factor variable ANOVA test (chosen for the singularity of the top/bottom zone factor, and the proliferation of multiple swings per 40+ different athletes), we see that the top/bottom factor is significant (with the p-value under null hypothesis F test registering < 0.000001) for swings under 100 degrees at connection of impact, whereas the subpopulation of swings with a higher connection at impact does not find the top/bottom denotation as being a significant explanatory variable for exit velocity (Pr(>F) = 0.32).
So, Contention B appears to be more valid when expanding its scope to the bottom of the zone as well.
Contention C
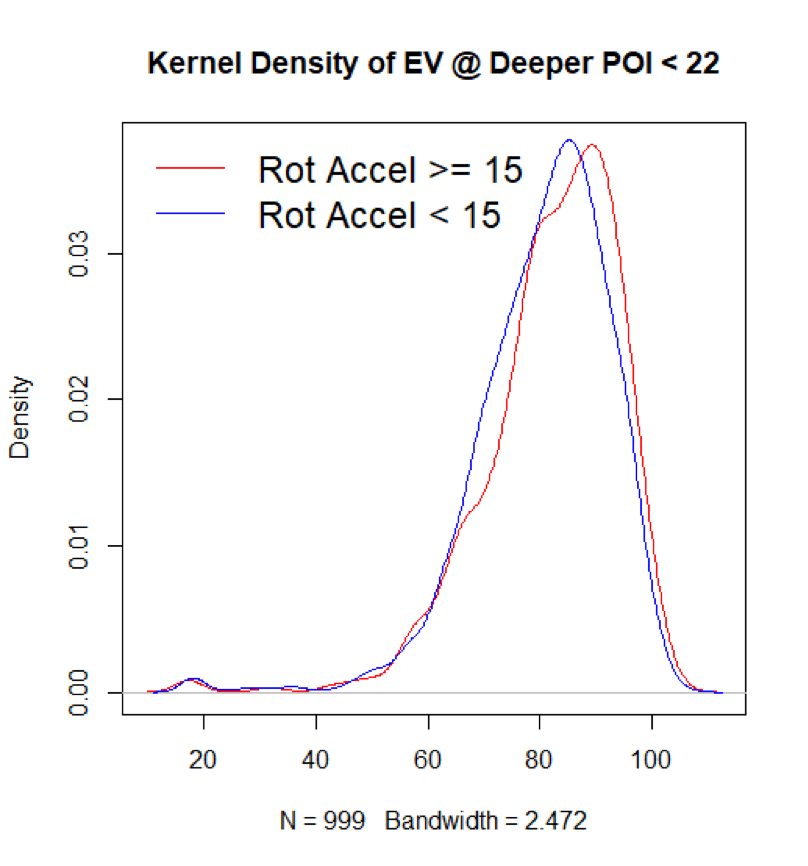
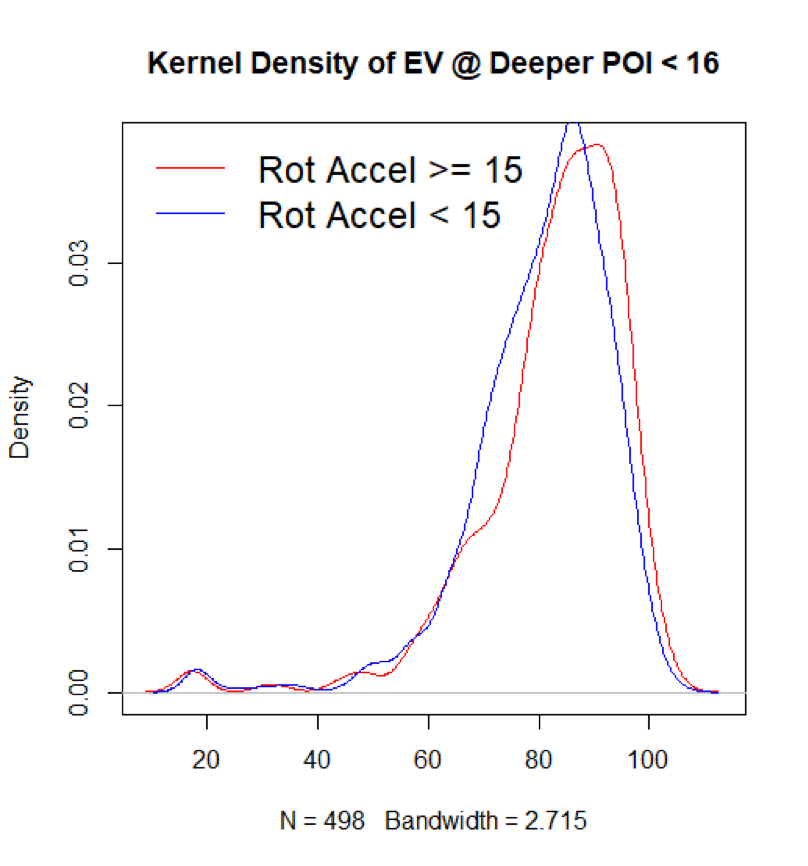
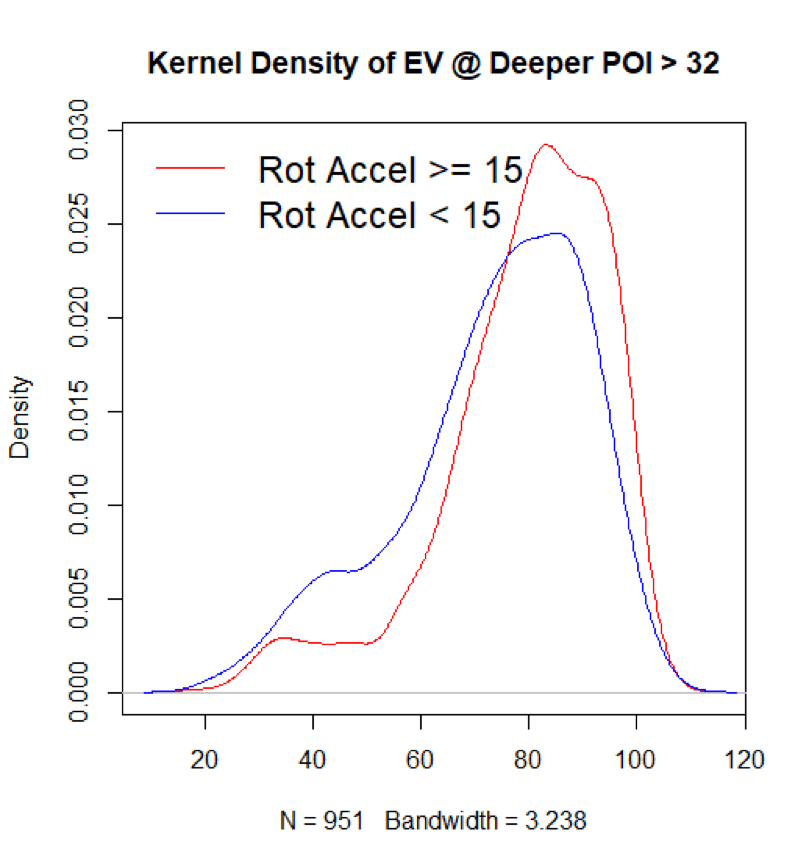
Athletes take too long to reach peak rotational speed during swing and will likely struggle to achieve high EV at deeper points of contact (for rotational_acceleration_<15).
Here, we’re varying three continuous metrics: rotational acceleration, point of impact depth, and exit velocity.
| POI Depth (in. Front of Plate) | Mean EV (Rot Accel >= 15) | Mean EV (Rot Accel < 15) |
| [14,18) | 82.75 | 80.67 |
| [18,22) | 81.63 | 81.00 |
| [22,26) | 82.34 | 80.81 |
| [26,30) | 83.03 | 80.64 |
| [30,34) | 81.62 | 78.97 |
| [34,38) | 82.15 | 77.58 |
| [38,42) | 79.83 | 74.35 |
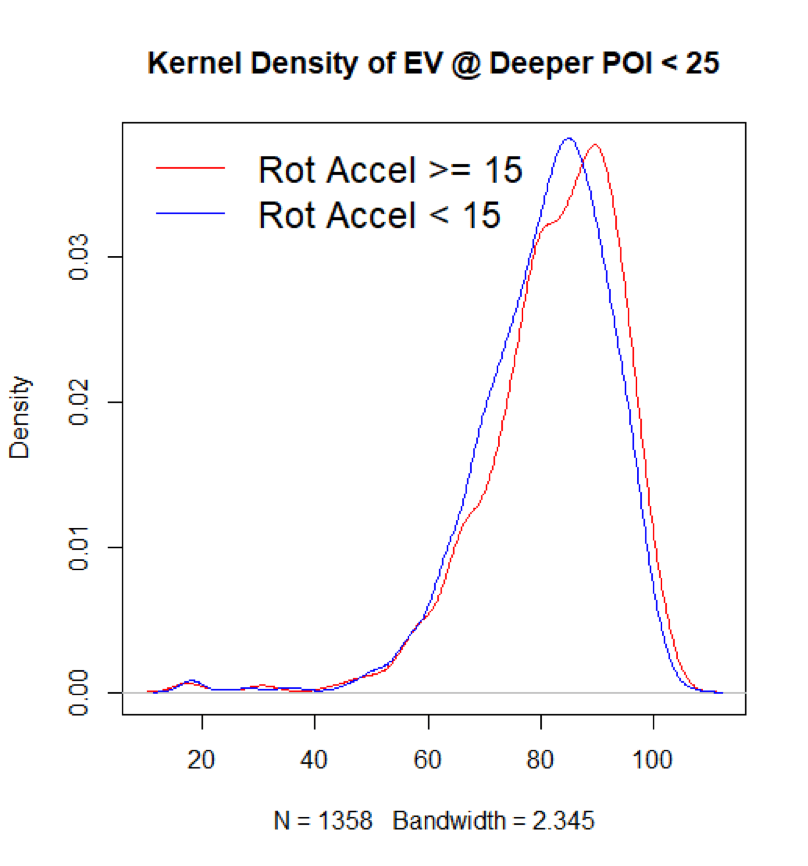
Having a lower rotational acceleration does seem to make it more difficult to achieve higher exit velocity at deeper points of contact—as well as at every other common point of contact. An examination of a few density plots of the two rotational acceleration populations seems to bear this out. But first, let’s look at three steadily deeper and more selective samples:
And then let’s consider a comparison at a shallow point of contact where the hitter is over two and a half feet out in front:
If anything, it looks like rotational acceleration becomes even more pivotal if the hitter is very out in front. Well there’s a happy takeaway: A higher rotational acceleration seems to speak dividends no matter where a hitter makes contact.
Contention D
The 1/8th rule average LA makes for a suitable proxy for attack angle on a macro scale (per hitter).
First, here is a little bit of explanation, since this may be a new theory to some. The idea (touched upon first here by Tom Tango and here in a community Fangraphs piece) implies that gathering a hitter’s hard-hit batted balls average launch angle is an appropriate benchmark for representing a hitter’s average attack angle. (A general proxy has been cited as the top eighth of hard-hit balls to serve as the said “hard hit batted balls” subgroup.) Now, this comparison has been analyzed and constructed roughly through thorough swing-mechanic reverse engineering, but now we have the chance to attempt to validate this method.
We have approximately 45 different hitters in our dataset but keeping in only those who have at least 40 batted ball events (so as to deal away with some small sample size snarkiness) leaves us with 39.
Then, we constructed three different attack angle proxies versus the actual average attack angle per hitter, and we calculated a few error results (mean absolute deviation and root mean square error) as well as a directional indicator of reliability (the ubiquitious R-squared).
Specifically, the proxies were computed as the following:
- Average launch angle of the hitter across all batted balls. (The simple and easy method.)
- The average launch angle of the 1/8th hardest hit balls (exit velocity) per hitter.
- An averaged of methods A and B.
| Proxy Method | AVG_Proxy | AVG_Attack_Angle | R^2 | MAD | RMSE |
| AVG_LA | 17.2169 | 5.8564 | 0.5001 | 11.4584 | 12.1844 |
| AVH_LA: 1/8th HHB | 10.7269 | 5.8564 | 0.5029 | 6.0512 | 7.1460 |
| Combo | 13.9719 | 5.8564 | 0.6104 | 8.4332 | 8.9950 |
These are fairly interesting results. Preferably, I would have also used the median LA as a proxy metric, but in this situation, with HitTrax representing launch angle as whole integers rather than float decimals, there wasn’t a discernable difference between the median and mean values.
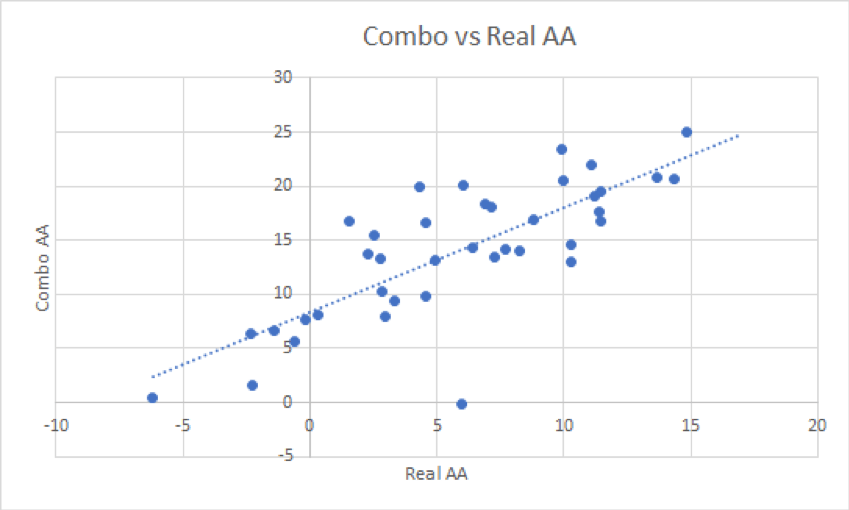
The real (as measured by HitTrax) attack angle has a magnitude difference with all off the proxies (a 5-degree difference with the second method and a ~8 degree difference with the third, combo method) but looks quite directionally reliable with strong correlation values. The combo method specifically looks very promising, given awareness of the magnitude difference—and to be fair, for most analysis purposes in the scope of comparison, both of intra- and inter-nature, directional reliability could well be much more valuable than a strict low RMSE or the like. Here’s a visual representation of the combo method plotted via the actual average attack angle of each individual hitter:
Now, more contentions will come soon as we fold in both Rapsodo Hitting (tons of exciting batted-ball spin explorations) and some synced K-Vest data as well. For those of you that made it to the bottom of this, congrats! The diamonding will continue in the next piece of synced batted-ball and swing-data exploration.
Written by Quantitative Analyst Alex Caravan
Comment section